题目内容
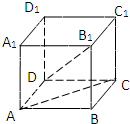
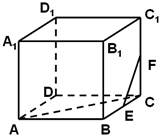
如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AA1,BB1的中点,求异面直线A1F与D1E所成角的余弦值.
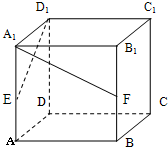

证明:连接A1C1、C1F、EF,
∵正方形AA1B1B中,E,F分别是棱AA1,BB1的中点,
∴A1B1∥EF且A1B1=EF
∵A1B1∥C1D1且A1B1=C1D1,
∴EF∥C1D1且EF=C1D1,可得四边形C1D1FE是平行四边形
因此,D1E∥C1F,
∴∠A1FC1(或其补角)就是异面直线A1F与D1E所成角
设正方体棱长为2,则△A1FC1中,A1F=C1F=
,A1C1=2
由余弦之理,得cos∠A1FC1=
=
>0
∴∠A1FC1是锐角,可得异面直线A1F与D1E所成角的余弦值为
.

∵正方形AA1B1B中,E,F分别是棱AA1,BB1的中点,
∴A1B1∥EF且A1B1=EF
∵A1B1∥C1D1且A1B1=C1D1,
∴EF∥C1D1且EF=C1D1,可得四边形C1D1FE是平行四边形
因此,D1E∥C1F,
∴∠A1FC1(或其补角)就是异面直线A1F与D1E所成角
设正方体棱长为2,则△A1FC1中,A1F=C1F=
| 5 |
| 2 |
由余弦之理,得cos∠A1FC1=
| 5+5-8 | ||||
2×
|
| 1 |
| 5 |
∴∠A1FC1是锐角,可得异面直线A1F与D1E所成角的余弦值为
| 1 |
| 5 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
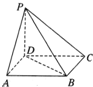
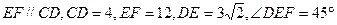 ,DA、CB都垂直于EF,且垂足分别为A,B,将梯形沿DA、CB折起,使E、F重合于点P,点M在AB上,且
,DA、CB都垂直于EF,且垂足分别为A,B,将梯形沿DA、CB折起,使E、F重合于点P,点M在AB上,且 。
。
 B
B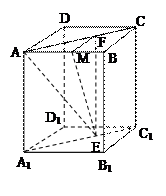 A.
A.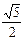 B.
B.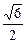 C.
C.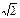 D.
D.