Question

如图，在正三棱柱ABC—A₁B₁C₁中,AB=AA₁，E是BB₁上的点，且平面A₁EC⊥平面AA₁C₁C.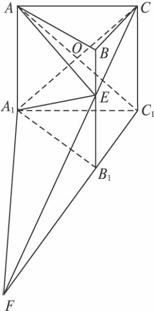

(1)确定点E的位置；

(2)若平面A₁EC与平面A₁B₁C₁所成的角为60°时，正三棱柱称为“黄金棱柱”，请判断此棱柱是否为“黄金棱柱”，并说明理由.

Answer 1

答案：解法一：(1)连结AC₁交A₁C于点O，连结AE、EC.

由于AB=AA₁，三棱柱ABC—A₁B₁C₁为正三棱柱，∴四边形AA₁C₁C为正方形.∴AO⊥A₁C.

∵平面A₁EC⊥平面AA₁C₁C且平面A₁EC∩平面AA₁C₁C=A₁C，

∴AO⊥平面A₁EC.∴AO⊥OE.                                                 

在△AEC₁中，AE=EC₁，

即.

而AB=B₁C₁，

∴BE=B₁E，即点E为棱BB₁的中点.                                            

(2)延长CE交C₁B₁的延长线于F，连结A₁F，

而B₁E∥C₁C，

∵.∴FB₁=B₁C₁.

∴FB₁=B₁C₁=A₁B₁.

∴FA₁⊥A₁C₁.                                                                

∵面AA₁C₁C⊥面A₁B₁C₁，面AA₁C₁C∩面A₁B₁C₁=A₁C₁，

∴FA₁⊥面AA₁C₁C，∴FA₁⊥CA₁，FA₁⊥C₁A₁.

∴∠CA₁C₁就是二面角CA₁FC₁的平面角.                                       

而∠CA₁C₁=45°≠60°，

∴此三棱柱不是“黄金棱柱”.

解法二：(1)如下图建立空间直角坐标系，设AB=AA₁=a，B₁E=b，

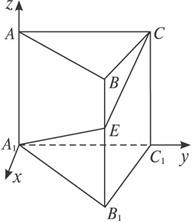
则A₁(0，0，0)、B₁(a,,0)、C₁(0，a，0)、E(a,,b)、C(0，a，a).           

∴=(a,,b),=(0,a,a).                                              

设平面A₁EC的法向量为m=(x，y，z)，则

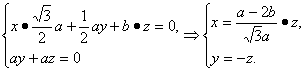
∴可取m=(,-1,1).                                                      

显然平面A₁C₁CA的法向量可取为n=(1，0，0).

由题意，平面A₁EC⊥平面AA₁C₁C，

∴m⊥n，∴m·n=0，即=0,b=.

∴点E为BB₁的中点.                                                         

(2)由(1)知，m=(0，-1，1)，显然平面A₁B₁C₁的法向量可取为l=(0，0，1)，

∴cos〈m,l〉=.                                            

∴〈m,l〉=45°.

∴平面A₁EC与平面A₁B₁C₁所成的锐二面角为45°，即此三棱柱不是“黄金棱柱”.