题目内容
ABCD是正方形，P是平面ABCD外一点，PD⊥AD，PD=AD=2，二面角P-AD-C为60°，则P到AB的距离是
- A.
- B.
- C.2
- D.
D
分析：要想求P到AB的距离要先证明AB⊥平面PEF，即PF⊥AB，根据题中已知条件求出PE的长度，再根据勾股定理便可求出PF的长度．
解答：
解：过P作PE⊥CD，过E作EF∥BC，连接PF，
∵AD⊥CD，PD⊥AD，
∴AD⊥平面PDC，
又∵PE在平面PDC上，∴AD⊥PE，
又∵PE⊥CD，∴PE⊥平面ABCD，
∴PE⊥AB
∵EF∥BC，∴AB⊥EF，
∴AB⊥平面PEF，∴PF⊥AB，
∴PF即为P到AB的距离，
∵∠PDC=60°，PD=2，∴PE=，
∵EF=AD=2，由勾股定理可得PF=
=．
故选D．
点评：本小题主要考查空间线面关系、二面角的度量、点线面距离的技计算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力，要求同学们熟练掌握．
分析：要想求P到AB的距离要先证明AB⊥平面PEF，即PF⊥AB，根据题中已知条件求出PE的长度，再根据勾股定理便可求出PF的长度．
解答：
解：过P作PE⊥CD，过E作EF∥BC，连接PF，∵AD⊥CD，PD⊥AD，
∴AD⊥平面PDC，
又∵PE在平面PDC上，∴AD⊥PE，
又∵PE⊥CD，∴PE⊥平面ABCD，
∴PE⊥AB
∵EF∥BC，∴AB⊥EF，
∴AB⊥平面PEF，∴PF⊥AB，
∴PF即为P到AB的距离，
∵∠PDC=60°，PD=2，∴PE=
，∵EF=AD=2，由勾股定理可得PF=
=．故选D．
点评：本小题主要考查空间线面关系、二面角的度量、点线面距离的技计算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力，要求同学们熟练掌握．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
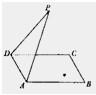ABCD是正方形，P是平面ABCD外一点，PD⊥AD，PD=AD=2，二面角P-AD-C为60°，则P到AB的距离是（ ）
Ｂ．
Ｃ．2 Ｄ．
是棱
的中点．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：
；
(2) 求证：
；
与直线
所成角的余弦值．
