题目内容
已知函数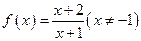 ,数列
,数列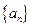 满足
满足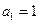 ,
,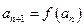 ,
,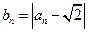 .
.
(1)求证: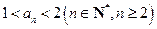 ;
;
(2)求证: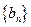 是递减数列;
是递减数列;
(3)设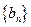 的前
的前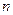 项和为
项和为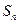 ,
,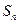 与
与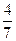 是否有确定的大小关系,如果有给出证明,如果没有给出反例.
是否有确定的大小关系,如果有给出证明,如果没有给出反例.
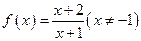 ,数列
,数列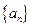 满足
满足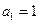 ,
,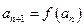 ,
,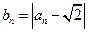 .
.(1)求证:
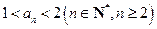 ;
;(2)求证:
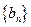 是递减数列;
是递减数列;(3)设
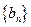 的前
的前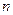 项和为
项和为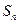 ,
,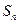 与
与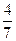 是否有确定的大小关系,如果有给出证明,如果没有给出反例.
是否有确定的大小关系,如果有给出证明,如果没有给出反例.(1)见解析(2)见解析(3)小于
由已知数列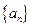 满足
满足 .
.
(1)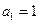 得
得 ,故
,故 ,假设
,假设 时,
时, ,
, ,
, ,
, ,则当
,则当 时,
时, ,由数学归纳知对一切
,由数学归纳知对一切 的正整数
的正整数 都成立.
都成立.
(2)
 ,故
,故 ,
,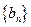 是递减数列.
是递减数列.
(3)由(2)得 ,
,
故 ,
,
所以

 .
.
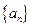 满足
满足 .
.(1)
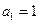 得
得 ,故
,故 ,假设
,假设 时,
时, ,
, ,
, ,
, ,则当
,则当 时,
时, ,由数学归纳知对一切
,由数学归纳知对一切 的正整数
的正整数 都成立.
都成立.(2)

 ,故
,故 ,
,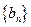 是递减数列.
是递减数列.(3)由(2)得
 ,
,故
 ,
,所以


 .
.
练习册系列答案
相关题目
 ,
, 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.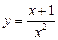 (
(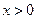 )上横坐标为1的点的切线方程为
)上横坐标为1的点的切线方程为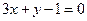
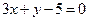
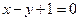
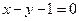
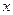 在9万元以下,没有奖金,
在9万元以下,没有奖金,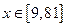 时,奖金为
时,奖金为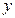 (万元),
(万元),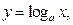
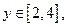 且年销售额
且年销售额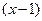 发奖金(年销售额
发奖金(年销售额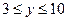 (万元),年销售额
(万元),年销售额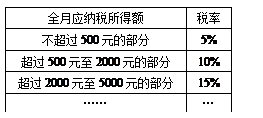
 ,函数
,函数 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; ,在
,在 处取得最大值,求
处取得最大值,求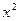 -4
-4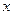 +2在点M(1,1)处的切线平行的直线方程是__________.
+2在点M(1,1)处的切线平行的直线方程是__________.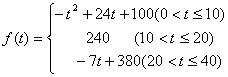
 在
在 处取到极值,那么实数
处取到极值,那么实数 的值为
的值为