题目内容
已知命题:“若数列{an}为等差数列,且am=a,an=b(m≠n,m,n∈N+),则 ”.现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=a,bn=b(m≠n,m,n∈N+).
”.现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=a,bn=b(m≠n,m,n∈N+).(1)请给出已知命的证明;
(2)类比(1)的方法与结论,推导出bm+n.
【答案】分析:(1)根据等差数列的性质可分别表示出am+n,联立方程求得am和an的值,代入原来的方程组中联立求得(m-n)am+n=ma-nb,则am+n的表达式可得.
(2)根据等差数列的性质可分别表示出bn+m,联立方程求得bm和bn的值,代入原来的方程组中联立求得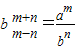 ,则bm+n的表达式可得.
,则bm+n的表达式可得.
解答:解:(1)因为在等差数列{an}中,由等差数列性质得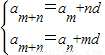 ,又am=a,an=b,
,又am=a,an=b,
∴ ,得
,得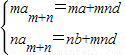 ,两式相减得(m-n)am+n=ma-nb,
,两式相减得(m-n)am+n=ma-nb,
∴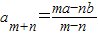 .
.
(2)在等比数列{bn}中,由等比数列的性质得 ,
,
又bm=a,bn=b,∴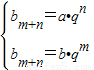 ,得
,得 ,两式相除得
,两式相除得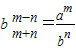 ,
,
∴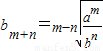 .
.
点评:本题主要考查了等比数列和等差数列的性质.考查了等比数列和等差数列通项公式的应用.
(2)根据等差数列的性质可分别表示出bn+m,联立方程求得bm和bn的值,代入原来的方程组中联立求得
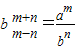 ,则bm+n的表达式可得.
,则bm+n的表达式可得.解答:解:(1)因为在等差数列{an}中,由等差数列性质得
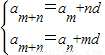 ,又am=a,an=b,
,又am=a,an=b,∴
 ,得
,得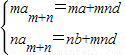 ,两式相减得(m-n)am+n=ma-nb,
,两式相减得(m-n)am+n=ma-nb,∴
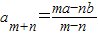 .
.(2)在等比数列{bn}中,由等比数列的性质得
 ,
,又bm=a,bn=b,∴
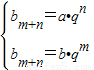 ,得
,得 ,两式相除得
,两式相除得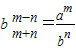 ,
,∴
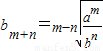 .
.点评:本题主要考查了等比数列和等差数列的性质.考查了等比数列和等差数列通项公式的应用.

练习册系列答案
相关题目