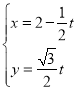Question

【题目】已知圆经过点，,且它的圆心在直线上.

（Ⅰ）求圆的方程;

（Ⅱ）求圆关于直线对称的圆的方程。

（Ⅲ）若点为圆上任意一点，且点,求线段的中点的轨迹方程.

Answer 1

【答案】（Ⅰ）（Ⅱ）（Ⅲ）

【解析】

试题分析：（Ⅰ）首先设出方程，将点坐标代入得到关于参数的方程组，通过解方程组得到参数值，从而确定其方程；（Ⅱ）求出N（2，4）关于x-y+3=0的对称点为（1，5），即可得到圆N关于直线x-y+3=0对称的圆的方程；（Ⅲ）首先设出点M的坐标，利用中点得到点D坐标，代入圆的方程整理化简得到的中点M的轨迹方程

试题解析：：（Ⅰ）由已知可设圆心N（a，3a-2），又由已知得|NA|=|NB|，

从而有，解得：a=2．

于是圆N的圆心N（2，4），半径．

所以，圆N的方程为．（5分）

（Ⅱ）N（2，4）关于x-y+3=0的对称点为（1，5），

所以圆N关于直线x-y+3=0对称的圆的方程为（9分）

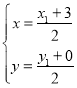（Ⅲ）设M（x，y），D，则由C（3，0）及M为线段CD的中点得：，解得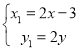又点D在圆N：上，所以有，

化简得：．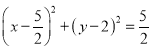

故所求的轨迹方程为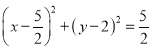．（13分）