题目内容
双曲线中心在原点,一条渐近线方程为 ,准线方程为
,准线方程为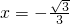 .
.
(1)求双曲线方程;
(2)若双曲线上存在关于y=kx+1对称的二点,求k范围.
解:(1)设双曲线方程为
由准线方程知
∴双曲线方程为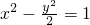
(2)设双曲线上关于y=kx+1对称二点为M(x1,y1)、N(x2,y2),其中点为Q(x0,y0)
设MN的方程为 代入
代入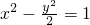
得
由 且
且
又Q(x0,y0)在直线y=kx+1
∴
∴
代入①式得22k4-13k2+1>0
∴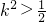 或
或  且
且
∴ ∪
∪ ∪
∪ ∪
∪
分析:(1)根据渐近线方程为 ,可假设方程为
,可假设方程为 ,再利用准线方程,可求双曲线方程;
,再利用准线方程,可求双曲线方程;
(2)设双曲线上关于y=kx+1对称二点为M(x1,y1)、N(x2,y2),其中点为Q(x0,y0),将MN的方程为 代入
代入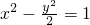 ,再利用Q(x0,y0)在直线y=kx+1,及判别式可求k范围.
,再利用Q(x0,y0)在直线y=kx+1,及判别式可求k范围.
点评:本题以双曲线为载体,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查对称性,有一定的综合性.

由准线方程知

∴双曲线方程为
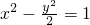
(2)设双曲线上关于y=kx+1对称二点为M(x1,y1)、N(x2,y2),其中点为Q(x0,y0)
设MN的方程为
 代入
代入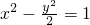
得

由
 且
且
又Q(x0,y0)在直线y=kx+1
∴

∴

代入①式得22k4-13k2+1>0
∴
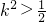 或
或  且
且
∴
 ∪
∪ ∪
∪ ∪
∪
分析:(1)根据渐近线方程为
 ,可假设方程为
,可假设方程为 ,再利用准线方程,可求双曲线方程;
,再利用准线方程,可求双曲线方程; (2)设双曲线上关于y=kx+1对称二点为M(x1,y1)、N(x2,y2),其中点为Q(x0,y0),将MN的方程为
 代入
代入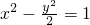 ,再利用Q(x0,y0)在直线y=kx+1,及判别式可求k范围.
,再利用Q(x0,y0)在直线y=kx+1,及判别式可求k范围.点评:本题以双曲线为载体,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查对称性,有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
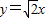 ,准线方程为
,准线方程为 .
. ,准线方程为
,准线方程为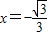 .
.