Question

已知数列{a_n}中，a₁=1，前n项和为S_n，且点P（a_n，a_n+1）（n∈N^*）在直线x-y+1=0上，则=________．

Answer 1

分析：根据点P（a_n，a_n+1）（n∈N^*）在直线x-y+1=0上，求出a_n的通项公式，然后再求出s_n的表达式，进而求得答案．
解答：∵点P（a_n，a_n+1）（n∈N^*）在直线x-y+1=0上，
∴a_n+1-a_n=1，
∴数列{a_n}是等差数列，
∵a₁=1，
∴s_n=，
∴=，
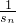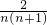∴=2（1--…-）=，
故答案为．
点评：本题主要考查数列求和的知识点，解答本题的关键是证明数列{a_n}是等差数列，然后求出等差数列的前n项和，然后在用裂项相消法求得．