题目内容
已知双曲线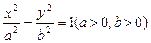
的左右两个焦点分别为
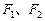,点P在双曲线右支上.
（Ⅰ）若当点P的坐标为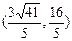
时,
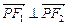,求双曲线的方程；
（Ⅱ）若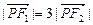
,求双曲线离心率
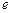的最值,并写出此时双曲线的渐进线方程.
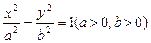的左右两个焦点分别为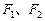,点P在双曲线右支上.（Ⅰ）若当点P的坐标为
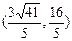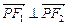时,,求双曲线的方程；（Ⅱ）若
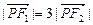,求双曲线离心率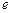的最值,并写出此时双曲线的渐进线方程.（Ⅰ）所求双曲线的方程为: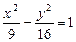 
（Ⅱ）双曲线的渐进线方程为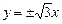
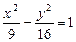
（Ⅱ）双曲线的渐进线方程为
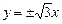
（Ⅰ）(法一)由题意知,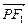
, 
,
,
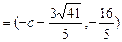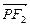
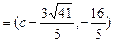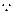
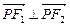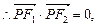
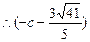
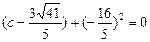（1分）
解得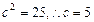
. 由双曲线定义得: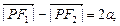 
,
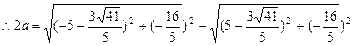
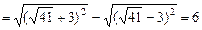所求双曲线的方程为: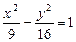
(法二) 因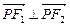,由斜率之积为
,可得解.
（Ⅱ）设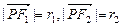
,
(法一)设P的坐标为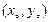
, 由焦半径公式得
,
,
，
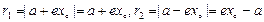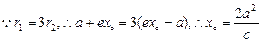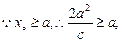
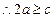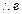的最大值为2,无最小值. 此时
,
此时双曲线的渐进线方程为
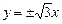
(法二)设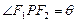
,
.
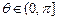(1)当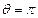
时,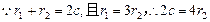 
, 
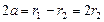
此时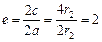
.
(2)当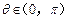
,由余弦定理得:
,
,
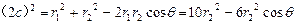
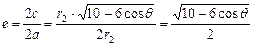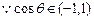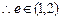,综上,
的最大值为2,但无最小值. (以下法一)
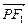
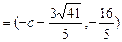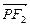
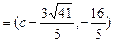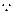
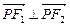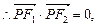
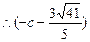
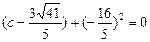, ,, （1分）解得
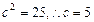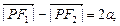
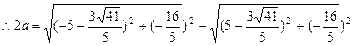
. 由双曲线定义得: 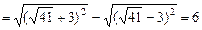, 所求双曲线的方程为: 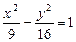(法二) 因
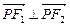,由斜率之积为,可得解.（Ⅱ）设
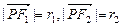,(法一)设P的坐标为
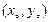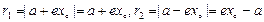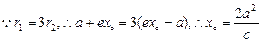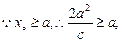
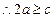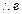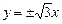
, 由焦半径公式得,,， 的最大值为2,无最小值. 此时,此时双曲线的渐进线方程为 (法二)设
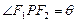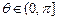,.(1)当
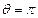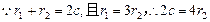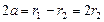
时, , 此时
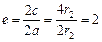.(2)当
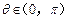,由余弦定理得: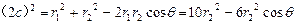 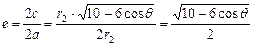,,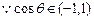,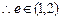综上,的最大值为2,但无最小值. (以下法一)
练习册系列答案
相关题目
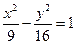的右顶点为A，右焦点为F，过点F平行双曲线的一条渐近线的直线与双曲线交于点B，则△AFB的面积为 。
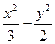=1截得的弦长为4,求直线l的方程.
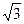,则∠F1PF2的大小为_________________.
-
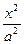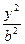=1的右支上有三点M、N、P,若这三点到右焦点的距离成等差数列,则它们的横坐标m、n、p( )
-
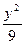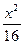=-1上的点M到点A（5，0）的距离为25，则M到点B（-5，0）的距离是___________________.
-
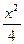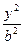=1(b∈N*)上,F1、F2为两焦点,若|PF1|、|F1F2|、|PF2|成等比数列,且|OP|<5,则b=_____________.
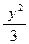=1上有一点P，使得|PA|+
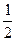|PF|最小，则点P的坐标是_______________.