题目内容
若当x∈(1,3)时,不等式ax<sin
x(a>0,a≠1)恒成立,则实数a的取值范围是( )
| π |
| 6 |
A、.(0,
| ||
B、.(0,
| ||
C、.[
| ||
D、[
|
分析:由题意当x∈(1,3)时,不等式ax<sin
x(a>0,a≠1)恒成立,就是函数y=sin
x的最小值,大于y=ax的最大值即可.
| π |
| 6 |
| π |
| 6 |
解答:解:因为y=sin
x在x∈(1,3)时,函数的增函数,所以它的最小值大于
,而y=ax的最大值为x=1时取得,并且恒成立,所以a≤
,
故选B
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B
点评:本题是基础题,考查三角函数的单调性,指数函数的单调性,恒成立问题的应用,考查计算能力,逻辑推理能力.

练习册系列答案
相关题目
 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是
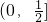
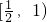

 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )


