题目内容
如图,线段AB(AB不与X轴垂直)过X轴上一点M(m,0)(m>0).端点A,B到X轴距离之积为2m,以X轴为对称轴,过A,O,B三点作抛物线.

(1)求抛物线方程;
(2)若tan∠AOB=-1,求m的取值范围
答案:
解析:
解析:
|
(1)当AB不垂直x轴时,设AB方程为y=k(x-m).抛物线方程为 由| (2)由 ∴| 又tg∠AOB=-1 即 平方后化简得 ∴m<6- ∴m的取值范围为0<m<6- |

练习册系列答案
相关题目
 =2px.(p>0)由
=2px.(p>0)由 得
得 -2py-2pkm=0,
-2py-2pkm=0,
 |=2m得p=1 ∴抛物线方程为
|=2m得p=1 ∴抛物线方程为 得
得 ,
, ,
, ,∴
,∴ =-1
=-1 ①
① -12m+4=
-12m+4= ∴
∴ 或m>6+
或m>6+ (2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k.
(2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k.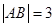 ,点M是线段AB上一点,且
,点M是线段AB上一点,且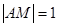 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动.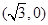 的直线
的直线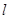 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若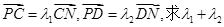 的值
的值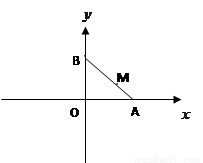
 ,点M是线段AB上一点,且
,点M是线段AB上一点,且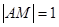 点M随线段AB的滑动而运动。
点M随线段AB的滑动而运动。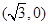 的直线
的直线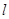 交曲线E于
交曲线E于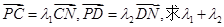 的值
的值
