题目内容
已知a为实数,x=1是函数 的一个极值点。
的一个极值点。
(Ⅰ)若函数 在区间
在区间 上单调递减,求实数m的取值范围;
上单调递减,求实数m的取值范围;
(Ⅱ)设函数 ,对于任意
,对于任意 和
和 ,有不等式
,有不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)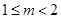 ; (Ⅱ)
; (Ⅱ)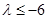 或
或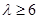
解析试题分析:(Ⅰ)由于x=1是函数的极值点,所以可以求出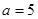 .即通过求导可以知道函数的单调递减区间(1,5).又由于函数
.即通过求导可以知道函数的单调递减区间(1,5).又由于函数 在区间
在区间 上单调递减.所以区间
上单调递减.所以区间 是区间(1,5)的子区间.即可得m的取值范围.
是区间(1,5)的子区间.即可得m的取值范围.
(Ⅱ)由不等式 恒成立.所以要先求出
恒成立.所以要先求出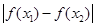 的最大值.即函数f(x)最大值与最小值相减的绝对值.另外的求出g(x)的最小值再解不等式.即可求得结论.本题的综合性较强,要理解清楚题意才能完整解答.
的最大值.即函数f(x)最大值与最小值相减的绝对值.另外的求出g(x)的最小值再解不等式.即可求得结论.本题的综合性较强,要理解清楚题意才能完整解答.
试题解析: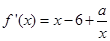 .(Ⅰ)
.(Ⅰ)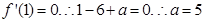 .首先x>0.得
.首先x>0.得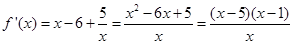 .令
.令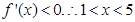 .即f(x)的单调递减区间是(1,5).因为f(x)在区间(2m-1,m+1)上单调递减.所以(2m-1,m+1)
.即f(x)的单调递减区间是(1,5).因为f(x)在区间(2m-1,m+1)上单调递减.所以(2m-1,m+1) 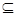 (1,5).所以
(1,5).所以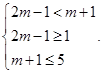
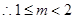 .
.
(Ⅱ)由(1).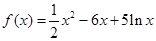 .列表如下:
.列表如下: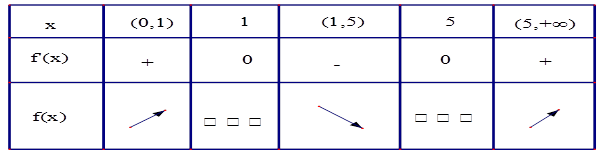
则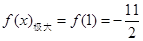 .
.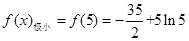 .所以
.所以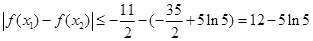 .所以
.所以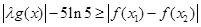 恒成立等价于
恒成立等价于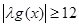 恒成立.因为
恒成立.因为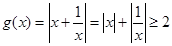 .当且仅当
.当且仅当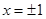 时取等号.所以
时取等号.所以 .所以
.所以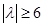 .所以
.所以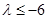 或
或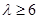 .
.
考点:1.函数求导.2.不等式恒成立的问题.3.单调性问题.4.绝对值的处理.

练习册系列答案
相关题目
 ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围. 为实常数,函数
为实常数,函数 .
. 的单调性;
的单调性; ;
; 且
且 .(注:
.(注: 为自然对数的底数)
为自然对数的底数) ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于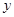 轴.
轴. 的值;
的值; 的极值.
的极值. ,若
,若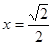 时,
时,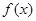 有极小值
有极小值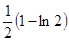 ,
,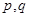 的取值;
的取值;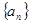 中,
中,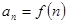 ,求证:数列
,求证:数列 项和
项和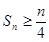 ;
;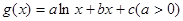 ,若
,若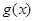 有极值且极值为
有极值且极值为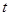 ,则
,则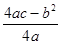 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论. ,
, ,其中
,其中 且
且 .
.  ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由. ,
,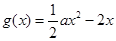 .
.
 在
在 与
与 处的切线相互平行,求
处的切线相互平行,求 的值及切线斜率;
的值及切线斜率; 上单调递减,求
上单调递减,求 的图像C1与函数
的图像C1与函数 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.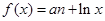 ,其中实数a为常数.
,其中实数a为常数. 的单调区间:
的单调区间: (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值; .
. 元,则销售量
元,则销售量 (单位:件)与零售价
(单位:件)与零售价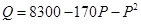 ,问该商品零售价定为多少元时毛利润
,问该商品零售价定为多少元时毛利润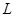 最大,并求出最大毛利润.(毛利润
最大,并求出最大毛利润.(毛利润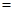 销售收入
销售收入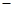 进货支出)
进货支出)