题目内容
曲线C的方程为
(p>0,t为参数),当t∈[-1,2]时,曲线C的端点为A,B,设F是曲线C的焦点,且S△AFB=14,求P的值.
|
把曲线C的方程
(p>0,t为参数),化为普通方程为 y2=2px.
当t∈[-1,2]时,曲线C的端点为A,B,可得A(2p,-2p)、B(8p,4p),
∴|AB|=
=6
p,
AB的方程为
=
,即 x-y-4p=0.
再根据曲线C的焦点F(
,0)到AB的距离为d=
=
.
再根据 S△AFB=14=
|AB|•d=
×6
p×
=14,解得 p=
.
|
当t∈[-1,2]时,曲线C的端点为A,B,可得A(2p,-2p)、B(8p,4p),
∴|AB|=
| (8p-2p)2+(4p+2p)2 |
| 2 |
AB的方程为
| y+2p |
| 4p+2p |
| x-2p |
| 8p-2p |
再根据曲线C的焦点F(
| p |
| 2 |
|
| ||
|
| 7p | ||
2
|
再根据 S△AFB=14=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 7p | ||
2
|
2
| ||
| 3 |

练习册系列答案
相关题目
 .
.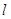 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线 是曲线C上的动点,求
是曲线C上的动点,求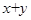 的最大值.
的最大值.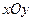 中,以
中,以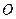 极点,
极点,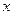 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为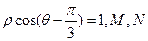 分别为
分别为 与
与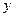 轴的交点
轴的交点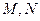 的极坐标
的极坐标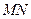 的中点为
的中点为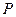 ,求直线
,求直线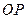 的极坐标方程
的极坐标方程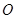 为极点、
为极点、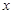 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点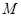 的极坐标为
的极坐标为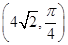 ,曲线
,曲线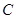 的参数方程为
的参数方程为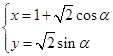 (
(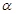 为参数),则点
为参数),则点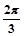 ,1)对应点的直角坐标是__________.
,1)对应点的直角坐标是__________.