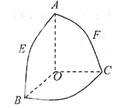
题目内容
已知曲线C1:
(t为参数),C2:
(θ为参数).
(Ⅰ)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)过曲线C2的左顶点且倾斜角为
的直线l交曲线C1于A,B两点,求|AB|.
|
|
(Ⅰ)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)过曲线C2的左顶点且倾斜角为
| π |
| 4 |
(1)∵C1:
(t为参数),C2:
(θ为参数),
∴消去参数得C1:(x+2)2+(y-1)2=1,C2:
+
=1,
曲线C1为圆心是(-2,1),半径是1的圆.
曲线C2为中心是坐标原点,焦点在x轴上,长轴长是8,短轴长是6的椭圆.
(2)曲线C2的左顶点为(-4,0),则直线l的参数方程为
(s为参数)
将其代入曲线C1整理可得:s2-3
s+4=0,设A,B对应参数分别为s1,s2,
则s1+s2=3
,s1s2=4,
所以|AB|=|s1-s2|=
=
.
|
|
∴消去参数得C1:(x+2)2+(y-1)2=1,C2:
| x2 |
| 16 |
| y2 |
| 9 |
曲线C1为圆心是(-2,1),半径是1的圆.
曲线C2为中心是坐标原点,焦点在x轴上,长轴长是8,短轴长是6的椭圆.
(2)曲线C2的左顶点为(-4,0),则直线l的参数方程为
|
将其代入曲线C1整理可得:s2-3
| 2 |
则s1+s2=3
| 2 |
所以|AB|=|s1-s2|=
| (s1+s2)2-4s1s2 |
| 2 |

练习册系列答案
相关题目
 上的动点
上的动点 是坐标为
是坐标为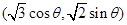 .
.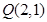 作曲线
作曲线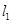 、
、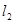 ,证明
,证明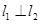 .
.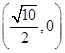 作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值.
作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值. 的参数方程为
的参数方程为 (
( 为参数),若以原点
为参数),若以原点 为极点,以
为极点,以 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆