题目内容
选做题:坐标系与参数方程已知直线l经过点P(2,3),倾斜角α=
 ,
,(Ⅰ)写出直线l的参数方程.
(Ⅱ)设l与圆x2+y2=4相交与两点A、B,求点P到A、B两点的距离之和.
【答案】分析:(1)根据直线的参数方程的特征及参数的几何意义,直接写出直线的参数方程.
(2)设点A,B的坐标分别为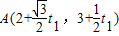 ,
,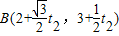 ,把直线L的参数方程代入圆的方程x2+y2=4整理得到
,把直线L的参数方程代入圆的方程x2+y2=4整理得到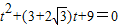 ①,由根与系数的关系
①,由根与系数的关系
可得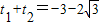 ,由t的几何意义可知|PA|+|PB|=|t1|+|t2|=-(t1+t2),从而求得结果.
,由t的几何意义可知|PA|+|PB|=|t1|+|t2|=-(t1+t2),从而求得结果.
解答:解:(1)由于过点(a,b) 倾斜角为α 的直线的参数方程为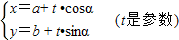 ,
,
∵直线l经过点P(2,3),倾斜角α=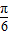 ,故直线的参数方程是
,故直线的参数方程是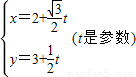 .…(5分)
.…(5分)
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为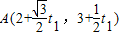 ,
,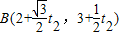 .
.
把直线L的参数方程代入圆的方程x2+y2=4整理得到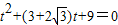 ①,…(8分)
①,…(8分)
因为t1和t2是方程①的解,从而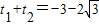 ,
,
由t的几何意义可知|PA|+|PB|=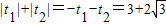 . …(10分)
. …(10分)
点评:本题主要考查直线的参数方程,以及直线的参数方程中参数的几何意义,直线和圆的位置关系的应用,属于基础题.
(2)设点A,B的坐标分别为
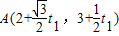 ,
,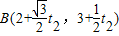 ,把直线L的参数方程代入圆的方程x2+y2=4整理得到
,把直线L的参数方程代入圆的方程x2+y2=4整理得到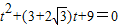 ①,由根与系数的关系
①,由根与系数的关系可得
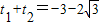 ,由t的几何意义可知|PA|+|PB|=|t1|+|t2|=-(t1+t2),从而求得结果.
,由t的几何意义可知|PA|+|PB|=|t1|+|t2|=-(t1+t2),从而求得结果.解答:解:(1)由于过点(a,b) 倾斜角为α 的直线的参数方程为
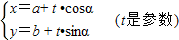 ,
,∵直线l经过点P(2,3),倾斜角α=
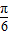 ,故直线的参数方程是
,故直线的参数方程是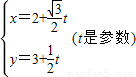 .…(5分)
.…(5分)(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为
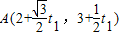 ,
,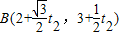 .
.把直线L的参数方程代入圆的方程x2+y2=4整理得到
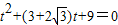 ①,…(8分)
①,…(8分)因为t1和t2是方程①的解,从而
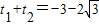 ,
,由t的几何意义可知|PA|+|PB|=
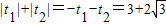 . …(10分)
. …(10分)点评:本题主要考查直线的参数方程,以及直线的参数方程中参数的几何意义,直线和圆的位置关系的应用,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 (t为参数)和圆C的极坐标方程:
(t为参数)和圆C的极坐标方程: .
.