题目内容
已知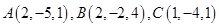 ,则向量
,则向量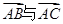 的夹角为 ( )
的夹角为 ( )
| A.30° | B.45° | C.60° | D.90° |
C
解析试题分析:因为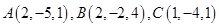 ,所以
,所以 (0,3,3),
(0,3,3), (-1,1,0),所以cos<
(-1,1,0),所以cos< ,
, >=
>= =
= =
= ,
,
又< ,
, >
> ,故向量
,故向量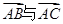 的夹角为60°,选C。
的夹角为60°,选C。
考点:本题主要考查空间向量的坐标运算,计算数量积、求夹角。
点评:基础题,计算向量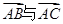 的夹角,要注意夹角的范围。
的夹角,要注意夹角的范围。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
如图,正四面体 的顶点
的顶点 分别在两两垂直的三条射线
分别在两两垂直的三条射线 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )
A. 是正三棱锥 是正三棱锥 |
B.直线 平面 平面 |
C.直线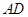 与 与 所成的角是 所成的角是 |
D.二面角 为 为 |
在空间直角坐标系中,已知 ,
, ,则
,则 ,
, 两点间的距离是
两点间的距离是
A. | B. | C. | D. |
设一地球仪的球心为空间直角坐标系的原点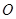 ,球面上有两个点
,球面上有两个点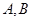 的坐标分别为
的坐标分别为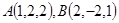 ,则
,则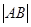 =( )
=( )
| A.18 | B.12 | C.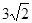 | D.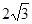 |
如图,在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点.若 =a,
=a, =b,
=b, =c,则下列向量中与
=c,则下列向量中与 相等的向量是
相等的向量是
A.- a+ a+ b+c b+c | B. a+ a+ b+c b+c |
C. a- a- b+c b+c | D.- a- a- b+c b+c |
如图:在平行六面体 中,
中, 为
为 与
与 的交点.若
的交点.若 ,
, ,
, 则下列向量中与
则下列向量中与 相等的向量是( )
相等的向量是( )
A. | B. |
C. | D. |
 与点
与点 的距离为 .
的距离为 .