题目内容
已知函数f(x)= 为奇函数,满足f(1)<f(3),且不等式0≤f(x)≤
为奇函数,满足f(1)<f(3),且不等式0≤f(x)≤ 的解集是[-2,-1]∪[2,4].
的解集是[-2,-1]∪[2,4].
(1)求a,b,c的值;
(2)对一切θ∈R,不等式f(-2+sinθ)≤m- 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.
解:(1)∵f(x)= 为奇函数∴
为奇函数∴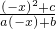 =-
=- ,解得b=0.…(2分)
,解得b=0.…(2分)
∵式0≤f(x)≤ 的解集中包含2和-2,
的解集中包含2和-2,
∴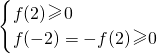
即得f(2)=0=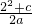 ,所以c=-4 …(4分)
,所以c=-4 …(4分)
∵f(1)<f(3),f(1)=- ,f(3)=-
,f(3)=-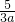 ,
,
∴- <
<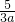 ,所以a>0…(5分)
,所以a>0…(5分)
下证:当a>0时,在(0,+∞)上f(x)=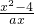 是增函数.
是增函数.
在(0,+∞)内任取x1,x2,且x1<x2,
那么f(x1)-f(x2)=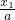 -
-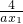 -
-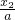 +
+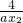 =
= (x1-x2)(1+
(x1-x2)(1+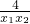 )<0
)<0
即f(x1)<f(x2),
∴当a>0时,在(0,+∞)上,f(x)=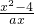 是增函数.
是增函数.
所以,f(2)=0,f(4)= =
=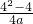 ,解得a=2.
,解得a=2.
综上所述:a=2,b=0,c=-4,f(x)=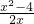 …(7分)
…(7分)
(2)∵f(x)= 为奇函数∴f(x)=
为奇函数∴f(x)= 在(-∞,0)上也是增函数.…(8分)
在(-∞,0)上也是增函数.…(8分)
又-3≤-2+sinθ≤-1,∴f(-3)≤f(-2+sinθ)≤f(-1)= …(10分)
…(10分)
而m- ≥
≥ …(12分)
…(12分)
所以,m≥3时,不等式f(-2+sinθ)≤m- 对一切θ∈R成立.…(13分)
对一切θ∈R成立.…(13分)
分析:(1)由f(x)为奇函数可得f(-x)=-f(x)可求b,由0≤f(x)≤ 的解集中包含2和-2,可得,f(2)≥0,
的解集中包含2和-2,可得,f(2)≥0,
f(-2)=-f(2)≥0即得f(2)=0,可求c,由f(1)<f(3),可得f(1)=- ,f(3)=-
,f(3)=-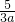 ,即-
,即- <
<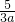 ,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=
,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=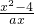 是增函数.由f(4)=
是增函数.由f(4)= =
=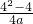 可求a
可求a
(2)由f(x)= 为奇函数可得f(x)=
为奇函数可得f(x)= 在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)=
在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)= ,从而可得m的取值范围
,从而可得m的取值范围
点评:本题综合考查了函数性质的应用:奇函数的定义及奇函数对称区间上的 单调性,利用定义证明函数的单调性,函数的恒成立与最值的相互转化的思想的体现.
 为奇函数∴
为奇函数∴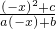 =-
=- ,解得b=0.…(2分)
,解得b=0.…(2分)∵式0≤f(x)≤
 的解集中包含2和-2,
的解集中包含2和-2,∴
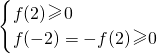
即得f(2)=0=
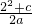 ,所以c=-4 …(4分)
,所以c=-4 …(4分)∵f(1)<f(3),f(1)=-
 ,f(3)=-
,f(3)=-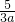 ,
,∴-
 <
<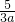 ,所以a>0…(5分)
,所以a>0…(5分)下证:当a>0时,在(0,+∞)上f(x)=
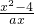 是增函数.
是增函数.在(0,+∞)内任取x1,x2,且x1<x2,
那么f(x1)-f(x2)=
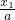 -
-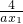 -
-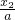 +
+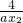 =
= (x1-x2)(1+
(x1-x2)(1+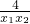 )<0
)<0即f(x1)<f(x2),
∴当a>0时,在(0,+∞)上,f(x)=
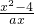 是增函数.
是增函数.所以,f(2)=0,f(4)=
 =
=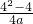 ,解得a=2.
,解得a=2.综上所述:a=2,b=0,c=-4,f(x)=
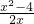 …(7分)
…(7分)(2)∵f(x)=
 为奇函数∴f(x)=
为奇函数∴f(x)= 在(-∞,0)上也是增函数.…(8分)
在(-∞,0)上也是增函数.…(8分)又-3≤-2+sinθ≤-1,∴f(-3)≤f(-2+sinθ)≤f(-1)=
 …(10分)
…(10分)而m-
 ≥
≥ …(12分)
…(12分)所以,m≥3时,不等式f(-2+sinθ)≤m-
 对一切θ∈R成立.…(13分)
对一切θ∈R成立.…(13分)分析:(1)由f(x)为奇函数可得f(-x)=-f(x)可求b,由0≤f(x)≤
 的解集中包含2和-2,可得,f(2)≥0,
的解集中包含2和-2,可得,f(2)≥0,f(-2)=-f(2)≥0即得f(2)=0,可求c,由f(1)<f(3),可得f(1)=-
 ,f(3)=-
,f(3)=-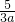 ,即-
,即- <
<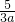 ,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=
,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=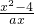 是增函数.由f(4)=
是增函数.由f(4)= =
=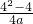 可求a
可求a(2)由f(x)=
 为奇函数可得f(x)=
为奇函数可得f(x)= 在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)=
在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)= ,从而可得m的取值范围
,从而可得m的取值范围点评:本题综合考查了函数性质的应用:奇函数的定义及奇函数对称区间上的 单调性,利用定义证明函数的单调性,函数的恒成立与最值的相互转化的思想的体现.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知函数f(x)=
函数f(x)在哪点连续( )
|
| A、处处连续 | ||
| B、x=1 | ||
| C、x=0 | ||
D、x=
|