Question

【题目】必修四第一章我们借助圆的对称性学习了诱导公式，如在直观上讲单位圆中，当两个角的终边关于轴对称时，这两个角的正弦值相等；再如在单位圆中，当两个角的终边关于原点中心对称时，这两个角的正弦值互为相反数.观察这些诱导公式，可以发现它们都是特殊角与任意角的三角函数的恒等关系.我们如果将特殊角换为任意角，那么任意角与的和(或差)的三角函数与，的三角函数会有什么关系呢？如果已知，的正弦余弦，能由此推出的正弦余弦吗？下面是某高一学生在老师的指导下自行探究与角的正弦余弦之间的关系的部分过程，请你顺着这位同学的思路以及老师的提示将探究过程完善，并完成后面的题目.探究过程如下：

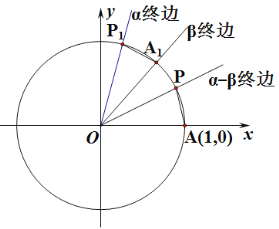
不妨令如图，设单位圆与轴的正半轴相交于点以轴的非负半轴为始边作角它们的终边分别与单位圆相交于点连接若把扇形绕着点旋转角，则点分别与点重合. ……(未完待续)

(提示一：任意一个圆绕着其圆心旋转任意角后都与原来的圆重合，这一性质叫做圆的旋转对称性)(提示二：平面上任意两点间的距离公式)

（1）完善上述探究过程；

（2）利用（1）中的结论解决问题：已知是第三象限角，求的值.

Answer 1

【答案】（1）见解析；（2）.

【解析】

（1）根据，利用两点间的距离公式，即可得到答案；

（2）分别求出，，再利用（1）中结论，即可得到答案；

（1），

，

整理得：；

（2）是第三象限角，

，，

.