题目内容
已知△ABC的面积S=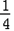 (b2+c2-a2),其中a,b,c分别为角A,B,C所对的边
(b2+c2-a2),其中a,b,c分别为角A,B,C所对的边
(1)求角A的大小.
(2)若a=2,求 的最大值.
的最大值.
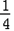 (b2+c2-a2),其中a,b,c分别为角A,B,C所对的边
(b2+c2-a2),其中a,b,c分别为角A,B,C所对的边(1)求角A的大小.
(2)若a=2,求
 的最大值.
的最大值.解:(1)由三角形面积公式可知S= bcsinA,
bcsinA,
∵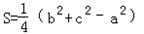 ,
,
∴ bcsinA=
bcsinA=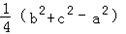
由余弦定理可知2bccosA=b2+c2﹣a2
∴sinA=cosA,即tanA=1,
又由A是三角形内角
∴A=45°
(2)∵由余弦定理可知2bccosA=b2+c2﹣a2,a=2,
即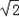 bc=b2+c2﹣4≥2bc﹣4
bc=b2+c2﹣4≥2bc﹣4
∴(2﹣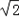 )bc≤4
)bc≤4
∴bc≤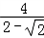 =4+2
=4+2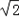
∴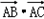 =
=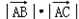 cosA=
cosA=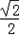 bc≤2+2
bc≤2+2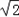
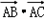 的最大值为2+2
的最大值为2+2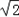
 bcsinA,
bcsinA,∵
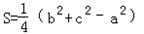 ,
,∴
 bcsinA=
bcsinA=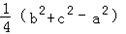
由余弦定理可知2bccosA=b2+c2﹣a2
∴sinA=cosA,即tanA=1,
又由A是三角形内角
∴A=45°
(2)∵由余弦定理可知2bccosA=b2+c2﹣a2,a=2,
即
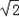 bc=b2+c2﹣4≥2bc﹣4
bc=b2+c2﹣4≥2bc﹣4∴(2﹣
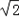 )bc≤4
)bc≤4∴bc≤
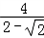 =4+2
=4+2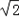
∴
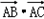 =
=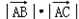 cosA=
cosA=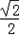 bc≤2+2
bc≤2+2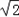
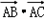 的最大值为2+2
的最大值为2+2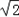

练习册系列答案
相关题目