题目内容
在△ABC中,BC=10,AB+AC=20,求sinB+sinC的最大值.
分析:由已知的BC积AB+AC的长,得到点A的轨迹为以B和C为焦点,且长轴2a=20,焦距2c=10的椭圆,画出相应的图形,根据图形可得三角形ABC为等边三角形时,sinB+sinC最大,进而求出此时的最大值.
解答:解:由BC=10,AB+AC=20可得:
点A在以B和C为焦点,且长轴2a=20,焦距2c=10的椭圆上,
根据题意画出图形,如图所示:
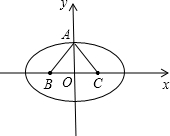
由图象可知:当△ABC为等边三角形时,sinB+sinC最大,
则sinB+sinC的最大值为2sin
=
.
点A在以B和C为焦点,且长轴2a=20,焦距2c=10的椭圆上,
根据题意画出图形,如图所示:

由图象可知:当△ABC为等边三角形时,sinB+sinC最大,
则sinB+sinC的最大值为2sin
| π |
| 3 |
| 3 |
点评:此题属于解三角形的题型,涉及的知识有轨迹方程,椭圆的定义,以及特殊角的三角函数值,利用了数形结合的思想,根据题意画出相应的图形是解本题的关键.

练习册系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |