题目内容
【题目】某农科院为试验冬季昼夜温差对反季节大豆新品种发芽的影响,对温差与发芽率之间的关系进行统计分析研究,记录了6天昼夜温差与实验室中种子发芽数的数据如下:
日期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 | 1月5日 | 1月6日 |
温差 | 10 | 11 | 12 | 13 | 8 | 9 |
发芽数 | 26 | 27 | 30 | 32 | 21 | 24 |
他们确定的方案是先从这6组数据中选出2组,用剩下的4组数据求回归方程,再用选取的两组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若由线性回归方程得到的估计数据与实际数据的误差不超过1粒,则认为得到的线性回归方程是可靠的.请根据1月2,3,4,5日的数据求出![]() 关于
关于![]() 的线性回归方程(保留两位小数),并检验此方程是否可靠.
的线性回归方程(保留两位小数),并检验此方程是否可靠.
参考公式: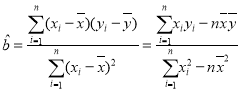 ,
,![]()
【答案】(1)![]() (2)
(2)![]() .可靠
.可靠
【解析】
(1)先求得从6组数据中任选2组数据的基本事件个数,再得相邻2天数据事件个数,即可得选取的2组数据恰好是相邻2天数据的概率;
(2)根据所给数据,分别求得![]() ,代入公式可得
,代入公式可得![]() ,进而得回归直线方程;分别再代入
,进而得回归直线方程;分别再代入![]() ,
,![]() 检验即可判断.
检验即可判断.
(1)从6组数据中任选2组数据,共有15个基本事件,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
记这2组数据恰好是相邻两天数据为事件A,
则A中有![]() ,共5个基本事件,
,共5个基本事件,
故![]() .
.
(2)![]() ,
,
![]() ,
,
所以![]()
![]() .
.
所求的回归方程为![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
故此线性回归方程是可靠的.

 考前必练系列答案
考前必练系列答案【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,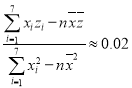 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,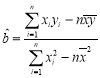 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.