Question

设函数f（x）的定义域为M，若函数f（x）满足条件[m，n]⊆M，使f（x）在[m，n]上的值域是[

m

2

，

n

2

]，则成f（x）为“半缩函数”，若函数f（x）=log₃（3^x+λ）为“半缩函数”，则λ的范围是（　　）

• A、（0，1）
• B、（0，

  1

  4

  ）
• C、（0，

  1

  2

  ]
• D、（

  1

  4

  ，+∞）

Answer 1

考点：函数的值域,函数的定义域及其求法

专题：计算题,作图题,函数的性质及应用

分析：由题意先判断f（x）=log₃（3^x+λ）在其定义域上是增函数，从而可得方程f（x）=

x

2

有两个不同的根，代入解λ的范围．

解答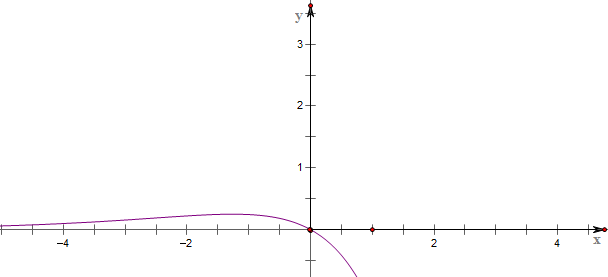： 解：由复合函数的单调性可知，
f（x）=log₃（3^x+λ）在其定义域上是增函数，
若由函数f（x）=log₃（3^x+λ）为“半缩函数”可知，
方程f（x）=

x

2

有两个不同的根，
即log₃（3^x+λ）=

x

2

有两个不同的根，
即3^x+λ=3

x

2

有两个不同的根，
则作函数λ=3

x

2

-3^x的图象可得，
结合选项可得，
λ∈（0，

1

4

）；
故选B．

点评：本题考查了学生对新定义的理解与应用，同时考查了函数性质应用，属于中档题．