题目内容
已知数列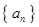 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,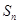 为其前n项和,且满足
为其前n项和,且满足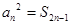 ,
,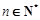 .数列
.数列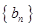 满足
满足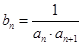 ,
,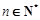 ,
, 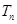 为数列
为数列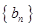 的前n项和.
的前n项和.
(1)求数列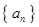 的通项公式
的通项公式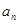 和数列
和数列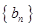 的前n项和
的前n项和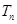 ;
;
(2)若对任意的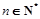 ,不等式
,不等式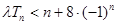 恒成立,求实数
恒成立,求实数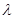 的取值范围;
的取值范围;
(3)是否存在正整数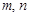
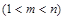 ,使得
,使得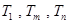 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有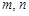 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
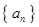 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,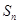 为其前n项和,且满足
为其前n项和,且满足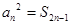 ,
,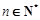 .数列
.数列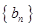 满足
满足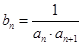 ,
,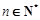 ,
, 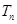 为数列
为数列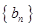 的前n项和.
的前n项和.(1)求数列
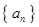 的通项公式
的通项公式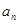 和数列
和数列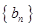 的前n项和
的前n项和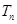 ;
;(2)若对任意的
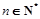 ,不等式
,不等式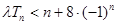 恒成立,求实数
恒成立,求实数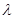 的取值范围;
的取值范围;(3)是否存在正整数
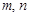
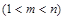 ,使得
,使得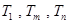 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有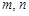 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)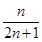
(2)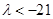 . ……9分
. ……9分
(3) 存在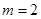

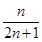
(2)
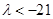 . ……9分
. ……9分(3) 存在
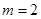

试题分析:(1)由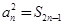 可令n=1,n=2得到关于a1与d的两个方程,从而可解出a1和d,得到an的通项公式.因为
可令n=1,n=2得到关于a1与d的两个方程,从而可解出a1和d,得到an的通项公式.因为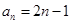 ,所以
,所以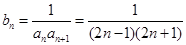 显然要采用裂项求和的方法求出其前n项和.
显然要采用裂项求和的方法求出其前n项和.
(2)因为本小题是关于n的不等式恒成立问题,应对n的奇偶进行讨论.分别再对得到的结果求交集.
(3)解本小题的关键由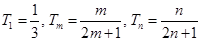 ,
,
若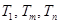 成等比数列,则
成等比数列,则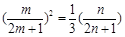 ,即
,即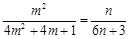 .
.
从而得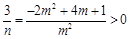 ,据此得到m的范围,找到m的值,进一步得到n的值.
,据此得到m的范围,找到m的值,进一步得到n的值.
解:(1)在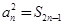 中,令
中,令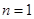 ,
,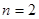 ,
,
得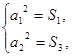 即
即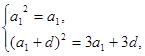 ……1分
……1分
解得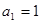 ,
,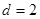 ,
,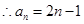 ……2分
……2分
又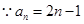 时,
时,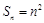 满足
满足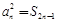 ,
,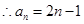
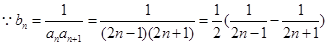 , ……3分
, ……3分
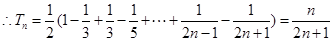 . ……4分
. ……4分
(2)①当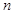 为偶数时,要使不等式
为偶数时,要使不等式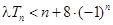 恒成立,即需不等式
恒成立,即需不等式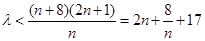 恒成立. ……5分
恒成立. ……5分
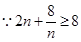 ,等号在
,等号在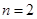 时取得
时取得
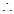 此时
此时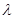 需满足
需满足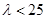 ……6分
……6分
②当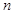 为奇数时,要使不等式
为奇数时,要使不等式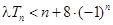 恒成立,即需不等式
恒成立,即需不等式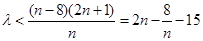 恒成立. ……7分
恒成立. ……7分
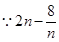 是随
是随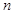 的增大而增大,
的增大而增大,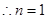 时
时 取得最小值
取得最小值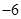 .
.
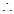 此时
此时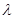 需满足
需满足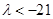 . ……8分
. ……8分
综合①、②可得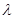 的取值范围是
的取值范围是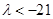 . ……9分
. ……9分
(3)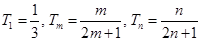 ,
,
若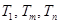 成等比数列,则
成等比数列,则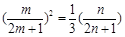 ,……10分
,……10分
即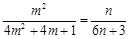 .
.
由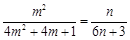 ,可得
,可得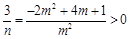 , ……12分
, ……12分
即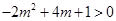 ,
,
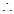
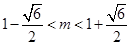 . ……13分
. ……13分
又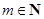 ,且
,且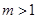 ,所以
,所以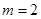 ,此时
,此时 .
.
因此,当且仅当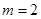 ,
, 时,数列
时,数列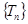 中的
中的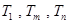 成等比数列. …14分
成等比数列. …14分
[另解] 因为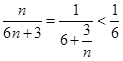 ,故
,故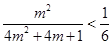 ,即
,即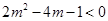 ,
,
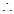
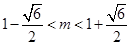 .
.
点评:(1)由an与Sn的关系求通项要注意根据需要给n赋值,每赋一个值就可得到一个方程.
(2)有关n的不等式恒成立问题,要注意题目当中如果有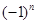 要注意按n为奇偶进行讨论.
要注意按n为奇偶进行讨论.
(3)解小题的关键是利用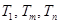 成等比数列,建立n与m的等式关系,下一步难点在于对式子的变形处理上,要注意体会其方法.
成等比数列,建立n与m的等式关系,下一步难点在于对式子的变形处理上,要注意体会其方法.
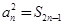 可令n=1,n=2得到关于a1与d的两个方程,从而可解出a1和d,得到an的通项公式.因为
可令n=1,n=2得到关于a1与d的两个方程,从而可解出a1和d,得到an的通项公式.因为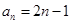 ,所以
,所以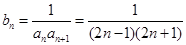 显然要采用裂项求和的方法求出其前n项和.
显然要采用裂项求和的方法求出其前n项和.(2)因为本小题是关于n的不等式恒成立问题,应对n的奇偶进行讨论.分别再对得到的结果求交集.
(3)解本小题的关键由
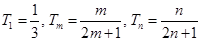 ,
,若
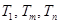 成等比数列,则
成等比数列,则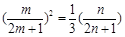 ,即
,即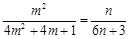 .
.从而得
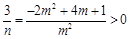 ,据此得到m的范围,找到m的值,进一步得到n的值.
,据此得到m的范围,找到m的值,进一步得到n的值.解:(1)在
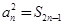 中,令
中,令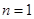 ,
,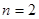 ,
,得
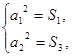 即
即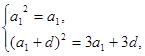 ……1分
……1分解得
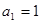 ,
,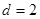 ,
,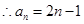 ……2分
……2分又
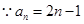 时,
时,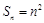 满足
满足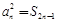 ,
,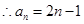
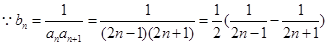 , ……3分
, ……3分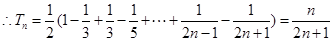 . ……4分
. ……4分(2)①当
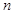 为偶数时,要使不等式
为偶数时,要使不等式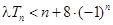 恒成立,即需不等式
恒成立,即需不等式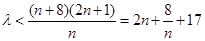 恒成立. ……5分
恒成立. ……5分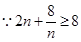 ,等号在
,等号在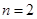 时取得
时取得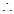 此时
此时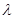 需满足
需满足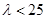 ……6分
……6分②当
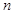 为奇数时,要使不等式
为奇数时,要使不等式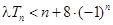 恒成立,即需不等式
恒成立,即需不等式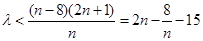 恒成立. ……7分
恒成立. ……7分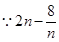 是随
是随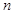 的增大而增大,
的增大而增大,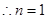 时
时 取得最小值
取得最小值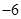 .
.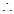 此时
此时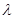 需满足
需满足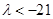 . ……8分
. ……8分综合①、②可得
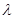 的取值范围是
的取值范围是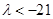 . ……9分
. ……9分(3)
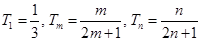 ,
,若
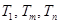 成等比数列,则
成等比数列,则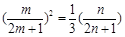 ,……10分
,……10分即
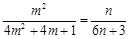 .
. 由
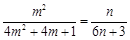 ,可得
,可得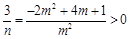 , ……12分
, ……12分即
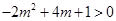 ,
,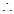
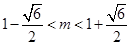 . ……13分
. ……13分 又
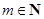 ,且
,且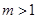 ,所以
,所以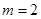 ,此时
,此时 .
.因此,当且仅当
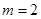 ,
, 时,数列
时,数列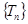 中的
中的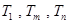 成等比数列. …14分
成等比数列. …14分[另解] 因为
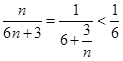 ,故
,故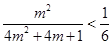 ,即
,即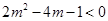 ,
,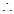
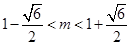 .
.点评:(1)由an与Sn的关系求通项要注意根据需要给n赋值,每赋一个值就可得到一个方程.
(2)有关n的不等式恒成立问题,要注意题目当中如果有
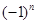 要注意按n为奇偶进行讨论.
要注意按n为奇偶进行讨论.(3)解小题的关键是利用
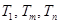 成等比数列,建立n与m的等式关系,下一步难点在于对式子的变形处理上,要注意体会其方法.
成等比数列,建立n与m的等式关系,下一步难点在于对式子的变形处理上,要注意体会其方法.
练习册系列答案
相关题目
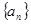 满足
满足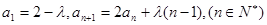
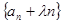 为等比数列;
为等比数列;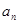 以及前n项和
以及前n项和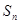 ;
;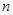 都有
都有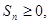 求
求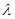 的取值范围。
的取值范围。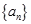 的前n项和为
的前n项和为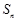 ,且满足
,且满足 ,
, =1,2,3,….
=1,2,3,….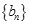 满足
满足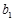 =1,且
=1,且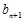 =
=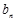 +
+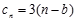 ,求数列
,求数列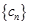 的前
的前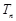 .
.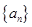 是公差不为零的等差数列,
是公差不为零的等差数列,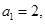 且
且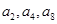 成等比数列
成等比数列 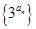 的前
的前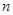 项和
项和  为等差数列
为等差数列 的前
的前 项的和,
项的和, ,
, ,则
,则 的值为( )
的值为( ) 




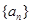 中,
中,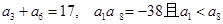 .
.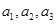 的顺序,使它成为等比数列
的顺序,使它成为等比数列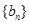 的前三项,求
的前三项,求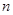 项和.
项和.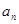 } 是等差数列,且
} 是等差数列,且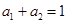 ,
,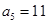 ,则数列{
,则数列{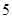 项的和
项的和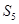 等于( )
等于( )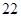
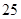
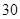
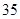
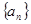 是等差数列,
是等差数列,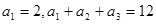
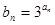 ,求数列
,求数列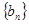 的前n项和Sn.
的前n项和Sn.