题目内容
7.设U=R,集合A={x|x2+3x+2<0},集合B={x|x2+(m+1)x+m<0},若B⊆A,则m的取值范围为1≤m≤2.分析 化简集合A,B,再由B⊆A可得-m≤-2,从而解得m的取值范围.
解答 解:A={x|x2+3x+2<0}=(-2,-1),B={x|(x+1)(x+m)<0},
∵B⊆A,
∴-1≥-m≥-2,
解得,1≤m≤2.
故答案为:1≤m≤2.
点评 本题考查了集合的化简与集合包含关系的应用,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{{log}_{\frac{1}{2}}x,x>1}\\{sinx,0≤x≤1}\\{\frac{x}{3},x<0}\end{array}\right.$,则下列结论中,正确的是( )
| A. | f(x)在区间(1,+∞)上是增函数 | B. | f(x)在区间(-∞,1]上是增函数 | ||
| C. | f($\frac{π}{2}$)=1 | D. | f(2)=1 |
17.设函数f(x)=x2-3x+1,则f(a)-f(-a)=( )
| A. | 0 | B. | -6a | C. | 2a2+2 | D. | 2a2-6a+2 |
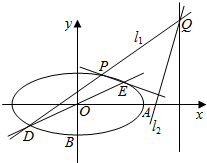 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过点A(a,0)与B(0,-b)的直线与原点的距离为$\frac{2\sqrt{10}}{5}$,又有直线y=$\frac{1}{2}$x与椭圆C交于D、E两点,过D点作斜率为k的直线l1与椭圆C的另一个交点为P,与直线x=4的交点为Q,过Q点作直线EP的垂线l2.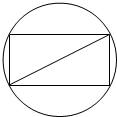 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?