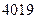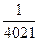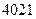题目内容
(本小题满分8分)
已知数列
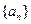 (
(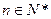 )的前
)的前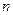 项的
项的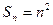 .
.
(Ⅰ)求数列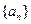 的通项公式;
的通项公式;
(Ⅱ)若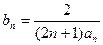 ,记数列
,记数列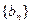 的前n项和为
的前n项和为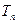 ,求使
,求使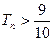 成立的最小正整数n的值。
成立的最小正整数n的值。
已知数列

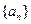 (
(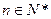 )的前
)的前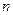 项的
项的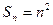 .
.(Ⅰ)求数列
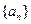 的通项公式;
的通项公式;(Ⅱ)若
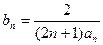 ,记数列
,记数列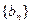 的前n项和为
的前n项和为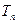 ,求使
,求使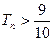 成立的最小正整数n的值。
成立的最小正整数n的值。解:(Ⅰ)∵ 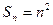
当 时,
时,
∴ 相减得:
又 符合上式
符合上式
∴ 数列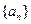 的通项公式
的通项公式
(II)由(I)知
∴


又
∴
∴ 成立的最小正整数n的值为5
成立的最小正整数n的值为5
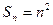
当
 时,
时,
∴ 相减得:

又
 符合上式
符合上式∴ 数列
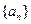 的通项公式
的通项公式
(II)由(I)知

∴



又

∴

∴
 成立的最小正整数n的值为5
成立的最小正整数n的值为5略

练习册系列答案
相关题目
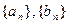 满足:
满足: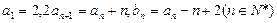
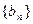 的通项公式;(2)设数列
的通项公式;(2)设数列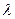 ,使得
,使得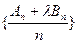 为等差数列?若存在,求出
为等差数列?若存在,求出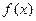 和数列
和数列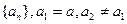 ,当
,当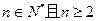 时,
时,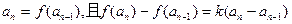 ,其中
,其中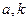 均为非零常数.
均为非零常数.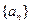 是等差数列,求
是等差数列,求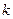 的值;
的值;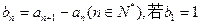 ,求数列
,求数列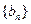 的通项公式;
的通项公式;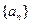 中,各项都是正数,且
中,各项都是正数,且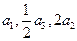 成等差数列,则
成等差数列,则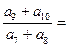
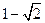
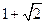
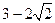
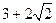
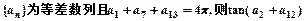 的值为 ( )
的值为 ( )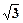
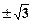
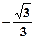
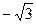
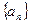 满足
满足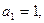
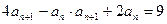
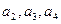 ;
;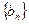 满足
满足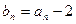 ,猜想数列
,猜想数列 中,若
中,若 ,
, ,则前9项的和
,则前9项的和 等于( )
等于( ) 66
66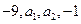
 四个实数成等差数列,
四个实数成等差数列,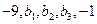 五个实数成等比数列,则
五个实数成等比数列,则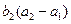 的值等于
的值等于 


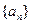 中,
中,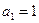 ,
,
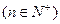 ,则
,则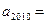 ( )
( )