题目内容
若函数 ,若a=f(3),b=f(4),c=f(5)则
,若a=f(3),b=f(4),c=f(5)则
- A.a<b<c
- B.c<b<a
- C.c<a<b
- D.b<a<c
B
分析:根据函数 ,得f(3)=ln
,得f(3)=ln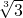 ,f(4)=ln
,f(4)=ln ,c=f(5)=ln
,c=f(5)=ln .通过根式的性质比较大小,得
.通过根式的性质比较大小,得 <
< <
<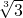 ,再结合y=lnx是定义在(0,+∞)上的增函数,可得ln
,再结合y=lnx是定义在(0,+∞)上的增函数,可得ln <ln
<ln <ln
<ln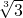 ,即c<b<a.
,即c<b<a.
解答:∵ ,
,
∴a=f(3)= =ln
=ln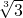 ,
,
同理可得b=f(4)=ln ,c=f(5)=ln
,c=f(5)=ln
∵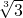 =
= =
= ,
, =
= =
=
∴ <
<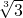
又∵ =
= =
= ,
, =
= =
=
∴ <
<
由此可得, <
< <
<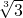
∵y=lnx是定义在(0,+∞)上的增函数
∴ln <ln
<ln <ln
<ln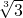 ,即c<b<a
,即c<b<a
故选B
点评:本题给出含有对数的分式函数,比较几个函数值的大小,着重考查了对数函数的单调性与根式比较大小等知识,属于基础题.
分析:根据函数
 ,得f(3)=ln
,得f(3)=ln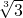 ,f(4)=ln
,f(4)=ln ,c=f(5)=ln
,c=f(5)=ln .通过根式的性质比较大小,得
.通过根式的性质比较大小,得 <
< <
<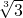 ,再结合y=lnx是定义在(0,+∞)上的增函数,可得ln
,再结合y=lnx是定义在(0,+∞)上的增函数,可得ln <ln
<ln <ln
<ln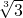 ,即c<b<a.
,即c<b<a.解答:∵
 ,
,∴a=f(3)=
 =ln
=ln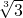 ,
,同理可得b=f(4)=ln
 ,c=f(5)=ln
,c=f(5)=ln
∵
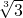 =
= =
= ,
, =
= =
=
∴
 <
<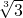
又∵
 =
= =
= ,
, =
= =
=
∴
 <
<
由此可得,
 <
< <
<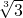
∵y=lnx是定义在(0,+∞)上的增函数
∴ln
 <ln
<ln <ln
<ln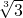 ,即c<b<a
,即c<b<a故选B
点评:本题给出含有对数的分式函数,比较几个函数值的大小,着重考查了对数函数的单调性与根式比较大小等知识,属于基础题.

练习册系列答案
相关题目
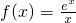 ,若a=f(3),b=f(4),c=f(5)则
,若a=f(3),b=f(4),c=f(5)则 ,若a=f(3),b=f(4),c=f(5)则( )
,若a=f(3),b=f(4),c=f(5)则( )