题目内容
14.$\underset{lim}{n→∞}$(1+$\frac{1}{2}$)•(1+$\frac{1}{{2}^{2}}$)•…•(1+$\frac{1}{{2}^{2n}}$)=2.分析 通过将(1+$\frac{1}{2}$)•(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{2n}}$)乘以$\frac{1-\frac{1}{2}}{1-\frac{1}{2}}$,对分子利用平方差公式化简可知(1+$\frac{1}{2}$)•(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{2n}}$)=2(1-$\frac{1}{{2}^{2n+1}}$),利用$\underset{lim}{n→∞}$$\frac{2}{{2}^{2n+1}}$=0计算即得结论.
解答 解:∵(1+$\frac{1}{2}$)•(1+$\frac{1}{{2}^{2}}$)•…•(1+$\frac{1}{{2}^{2n}}$)
=$\frac{(1-\frac{1}{2})(1+\frac{1}{2})(1+\frac{1}{{2}^{2}})•…•(1+\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$
=2(1-$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{2}}$)•…•(1+$\frac{1}{{2}^{2n}}$)
=…
=2(1-$\frac{1}{{2}^{2n+1}}$),
∴$\underset{lim}{n→∞}$(1+$\frac{1}{2}$)•(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{2n}}$)
=$\underset{lim}{n→∞}$2(1-$\frac{1}{{2}^{2n+1}}$)
=2-$\underset{lim}{n→∞}$$\frac{2}{{2}^{2n+1}}$
=2-$\underset{lim}{n→∞}$$\frac{1}{{2}^{2n}}$
=2-0
=2,
故答案为:2.
点评 本题考查极限及其运算,对表达式的灵活变形、利用平方差公式是解决本题的关键,注意解题方法的积累,属于中档题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | 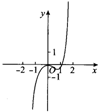 | B. | 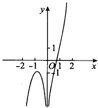 | C. | 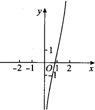 | D. | 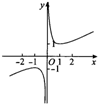 |
| A. | x2=$\frac{9}{2}$y | B. | y2=$\frac{4}{3}$x | C. | y2=$\frac{4}{3}$x或 x2=$\frac{9}{2}$y | D. | y2=$\frac{3}{4}$x或x2=$\frac{2}{9}$y |