题目内容
已知a、b、c均为正数,3a=4b=6c,求证:
解析:本题主要考查对数的定义及其运算性质.从求证的结论看,解题的关键是设法把a、b、c从连等号式中分离出来,为便于找出a,b,c的关系,不妨设3a=4b=6c=k(k>0),则a、b、c就可用这一变量k表示出来,再结合对数的运算性质就可证得结论.
证明:设3a=4b=6c=k,则k>0.由对数的定义得a=log3k,b=log4k,c=log6k,
则左边=![]() =2logk3+logk4=logk9+logk4=logk36,
=2logk3+logk4=logk9+logk4=logk36,
右边=![]() =2logk6=logk36,∴
=2logk6=logk36,∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
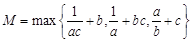 ,则M的最小值为 .
,则M的最小值为 .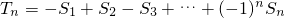 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;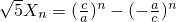 (n∈N+),证明:数列{
(n∈N+),证明:数列{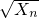 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.