题目内容
命题p:∃x∈R,使得x2+(a﹣1)x+1<0,命题q:∀x∈R,ax2+x+1>0恒成立.若p或q为真命题,p且q为假命题,求实数a的取值范围.
考点:
复合命题的真假.
专题:
阅读型.
分析:
根据题意分析:∃x∈R,使得x2+(a﹣1)x+1<0的条件与ax2+x+1>0恒成立的条件,求出命题P,命题q为真命题的a的范围;再根据复合命题的真值表,结合数形结合思想求解.
解答:
解:命题p为真,则△=(a﹣1)2﹣4>0⇒a>3或a<﹣1
命题q为真,则![]() ⇒a>
⇒a>![]()
∵p或q为真命题,p且q为假命题,根据复合命题的真值表,命题p和命题q一真一假

(1)命题p真,命题q假,则 ⇒a<﹣1
⇒a<﹣1
(2)命题p假,命题q真,则 ⇒
⇒![]()
综合得:a<﹣1或![]()
点评:
本题考查复合命题的真假判断.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
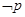 :∃x∈R,
:∃x∈R,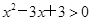 ,且
,且 ,则一元二次方程
,则一元二次方程 有实根”的逆否命题是真命题
有实根”的逆否命题是真命题 0;则
0;则 p:∀x∈R,均有x2+x+1
p:∀x∈R,均有x2+x+1 0
0 为假,则命题
为假,则命题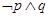 为真,
为真, 为假
为假 B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”
B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”