��Ŀ����
������Ա�����˵�վ���ij�����![]() �߷���Σ�յ�����ÿ��ֻ��һ���˽�ȥ����ÿ����ֻ��һ�Σ�����ʱ�䲻����10���ӣ������һ����10�����ڲ��������������������һ���ˡ�����һ��ֻ�мס��ҡ��������˿��ɣ����Ǹ������������ĸ��ʷֱ�
�߷���Σ�յ�����ÿ��ֻ��һ���˽�ȥ����ÿ����ֻ��һ�Σ�����ʱ�䲻����10���ӣ������һ����10�����ڲ��������������������һ���ˡ�����һ��ֻ�мס��ҡ��������˿��ɣ����Ǹ������������ĸ��ʷֱ�![]()
![]() ������
������![]() ������ȣ��Ҽٶ������ܷ����������¼������.
������ȣ��Ҽٶ������ܷ����������¼������.
��������������ȣ��Ҵ�֮��������˳�����ˣ��������ܱ���ɵĸ��ʡ����ı������˱��ɳ����Ⱥ�˳�������ܱ���ɵĸ����Ƿ����仯��
��������ijָ��˳�����ˣ��������˸������������ĸ�������Ϊ![]() ������
������![]() ��
��![]() ��һ�����У��������ɳ���Ա��
��һ�����У��������ɳ���Ա��![]() Ŀ
Ŀ![]() �ķֲ��к;�ֵ������������
�ķֲ��к;�ֵ������������![]() ��
��
���ٶ�![]() ���Է�����������
���Է�����������![]() �Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ�������������ﵽ��С��
�Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ�������������ﵽ��С��
�⣺��1��P=P1+��1-P1��P2+��1-P1����1-P2��P3
=P1+P2+P3-P1P2-P2P3-P3P1+P1P2P3
��������ɵĸ��ʲ������仯��
��2��X=1,2,3
| x | 1 | 2 | 3 |
| P | q1 | (1-q1)q2 | (1-q1)��1-q2�� |
Ex=q1q2+3-2q1-q2=��2-q2����1-q1)+1
(3)��q1>q2ʱ��q1q2+3-2q1-q2��-��q1q2+3-2q2-q1��=q2-q1<0
�����ɼף������ң�����ɱ���

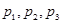
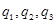 ������
������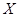 �ķֲ��к;�ֵ������������
�ķֲ��к;�ֵ������������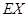 ��
��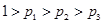 ���Է������������Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ�������������ﵽ��С��
���Է������������Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ�������������ﵽ��С��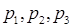 ������
������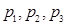 ������ȣ��Ҽٶ������ܷ����������¼������.
������ȣ��Ҽٶ������ܷ����������¼������.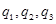 ������
������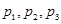 ��һ�����У��������ɳ���Ա��Ŀ
��һ�����У��������ɳ���Ա��Ŀ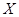 �ķֲ��к;�ֵ����ѧ������
�ķֲ��к;�ֵ����ѧ������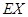 ��
��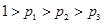 ���Է������������Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ����ѧ�������ﵽ��С����֤��֮��
���Է������������Ⱥ�˳���ɳ���Ա����ʹ�����ɳ�����Ա��Ŀ�ľ�ֵ����ѧ�������ﵽ��С����֤��֮��