题目内容
四棱锥 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2) 是
是 上的动点,
上的动点, 与平面
与平面 所成的最大角为
所成的最大角为 ,求二面角
,求二面角 的正切值.
的正切值.
(1)参考解析;(2)
解析试题分析:(1)由已知可得直线AE垂直于BC,即可得到AE垂直于AD,又因为PA垂直于AE.所以可得AE垂直于平面PAD.即可得平面要证平面 ⊥平面
⊥平面 .
.
(2)通过点E作EG垂直于AF,EQ垂直于AC,连结QG即可证得 为所求的二面角的平面角.由
为所求的二面角的平面角.由 与平面
与平面 所成的最大角为
所成的最大角为 .可得AE=AH.即可得EQ,QG的大小.从求得
.可得AE=AH.即可得EQ,QG的大小.从求得 的正切值,即二面角
的正切值,即二面角  的正切值.
的正切值.
(1)设菱形ABCD的边长为2a,则 AE=
AE=
 ,∴AE⊥BC,又AD||BC, ∴AE⊥AD.∵PA⊥面ABCD, ∴PA⊥AE,AE⊥面PAD, ∴面AEF⊥面PAD.
,∴AE⊥BC,又AD||BC, ∴AE⊥AD.∵PA⊥面ABCD, ∴PA⊥AE,AE⊥面PAD, ∴面AEF⊥面PAD.
(2)过E作EQ⊥AC,垂足为Q,过作QG⊥AF,垂足为G,连GE,∵PA⊥面ABCD,∴PA⊥EQ,EQ⊥面PAC,则∠EGQ是二面角E-AF-C的平面角.
过点A作AH⊥PD,连接EH,∵ AE⊥面PAD,∴∠AHE是EH与面PAD所成的最大角.
∵∠AHE= ,∴AH=AE=
,∴AH=AE= ,AH﹒PD=PA﹒AD,2a﹒PA=
,AH﹒PD=PA﹒AD,2a﹒PA= ﹒
﹒ ,PA=2
,PA=2 ,PC=4a,EQ=
,PC=4a,EQ= ,CQ=
,CQ= ,GQ=
,GQ= ,tan∠EGQ=
,tan∠EGQ= .
.
考点:1.面面垂直的判定.2.动点问题.3.二面角问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 是菱形,
是菱形, 是矩形,
是矩形, 面
面 .
.
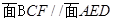 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积.
 ,D是AC的中点.
,D是AC的中点.


 中,
中,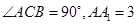 ,
,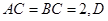 为
为 中点,
中点, 上一点,且
上一点,且 .
.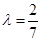 时,求证:
时,求证: 平面
平面 ;
; 与平面
与平面 所成的角为
所成的角为 ,求
,求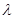 的值.
的值.
 是母线
是母线 的中点,
的中点, 是底面圆的直径,底面半径
是底面圆的直径,底面半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 时,求异面直线
时,求异面直线 与
与 所成的角;
所成的角; 的体积最大时,求
的体积最大时,求 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
 两点间的距离;
两点间的距离; 平面
平面 ;
; 所成角的正弦值.
所成角的正弦值.