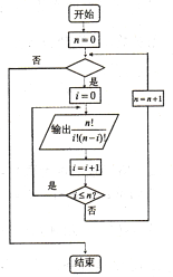
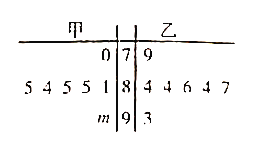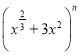题目内容
【题目】某地区2020年清明节前后3天每天下雨的概率为70%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数
（
，且
）表示是否下雨：当
时表示该地区下雨，当
时，表示该地区不下雨，从随机数表中随机取得20组数如下：
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
（1）求出
的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
（2）从2011年开始到2019年该地区清明节当天降雨量（单位：
）如下表：（其中降雨量为0表示没有下雨）.
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明：从2011年开始至2020年， 该地区清明节有降雨的年份的降雨量
与年份
成线性回归，求回归直线
，并计算如果该地区2020年（
）清明节有降雨的话，降雨量为多少？（精确到0.01）
参考公式：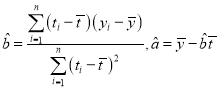
.
参考数据：
，
，
，
.
【答案】（1）
,
;（2）
,
．
【解析】
（1）根据每天下雨概率可求得
，在所给20组数确定表示3天中恰有2天下雨的组数，然后计算概率；
（2）计算
，根据所给数据求出回归直线方程中的系数，得回归直线方程，令
可得2020年的预估值．
（1）由
得，
即
表示下雨，
表示不下雨，
所给20组数中有714，740，945，593，468，491，272，073，951，169，027
共11组表示3天中恰有两天下雨，
∴所求概率为.
（2）由所给数据得
，
，
，
，
∴回归直线方程为：，
时，
，
∴2020年清明节有降雨的话，降雨量约为．
练习册系列答案
相关题目
