Question

将自然数1,2,3,4,…排成数阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…,则转第100个弯处的数为               .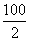

Answer 1

2 551

解法一:观察图中数表,第1次转弯加1,第2次转弯加1,第3次转弯加2,第4次转弯加2,第5次转弯加3,第6次转弯加3,第7次转弯加4,第8次转弯加4,…,依次可归纳出第99次和第100次转弯同在前一次转弯处加50,故第100次转弯处的整数为

1+(1+1)+(2+2)+(3+3)+(4+4)+…+(50+50)=1+2(1+2+3+…+50)=2 551.

解法二:观察数阵中“回”字形左对角线的数字,组成的数列{a_n}:1,3,7,13,21,….

则a_n-a_n-1=2(n-1),其中a₁=1(n∈N^*),用逐差法可求a_n.

∴a_n=n(n-1)+1.又此对角线转弯的次数均为偶数次,第2次转弯为a₂,第4次转弯为a₃,第6次转弯为a₄,第8次转弯为a₅,…,第100次转弯为a_n中第+1=51项,即第100次转弯为a₅₁=50×51+1=2 551.