题目内容
(本小题满分12分)已知集合A={x∣x2-3(a+1)x+2(3a+1)<0},B= ,
,
(1)当a=2时,求A∩B;
(2)求使BÍA的实数a的取值范围.
 ,
,(1)当a=2时,求A∩B;
(2)求使BÍA的实数a的取值范围.
(1) ;(2)[1,3]∪{-1}.
;(2)[1,3]∪{-1}.
 ;(2)[1,3]∪{-1}.
;(2)[1,3]∪{-1}.本试题主要是考查了一元二次不等式的求解,以及集合的交集和集合间关系的运用。
(1)根据已知条件先分析当a=2时,A=(2,7)B=(4,5)
得到结论。
(2)∵B=(2a,a2+1)那么根据 ,需要对于参数a进行分类讨论得到结论。
,需要对于参数a进行分类讨论得到结论。
解:(1)当a=2时,A=(2,7)B=(4,5)
∴ …………4分
…………4分
(2)∵B=(2a,a2+1), …………5分
①当a< 时,A=(3a+1,2)
时,A=(3a+1,2)
要使 必须
必须  …………7分
…………7分
② …………9分
…………9分
③a> 时,A=(2,3a+1)要使
时,A=(2,3a+1)要使 ,
,
必须 . …………11分
. …………11分
综上可知,使 的实数a的范围为[1,3]∪{-1}. …………12分
的实数a的范围为[1,3]∪{-1}. …………12分
(1)根据已知条件先分析当a=2时,A=(2,7)B=(4,5)
得到结论。
(2)∵B=(2a,a2+1)那么根据
 ,需要对于参数a进行分类讨论得到结论。
,需要对于参数a进行分类讨论得到结论。解:(1)当a=2时,A=(2,7)B=(4,5)
∴
 …………4分
…………4分(2)∵B=(2a,a2+1), …………5分
①当a<
 时,A=(3a+1,2)
时,A=(3a+1,2)要使
 必须
必须  …………7分
…………7分②
 …………9分
…………9分③a>
 时,A=(2,3a+1)要使
时,A=(2,3a+1)要使 ,
,必须
 . …………11分
. …………11分综上可知,使
 的实数a的范围为[1,3]∪{-1}. …………12分
的实数a的范围为[1,3]∪{-1}. …………12分
练习册系列答案
相关题目
 ,
, .
. ;
; 的不等式
的不等式 的解集是B,求
的解集是B,求 的值.
的值. ,求
,求 成立时
成立时 的取值范围。
的取值范围。 ,
, ,
, ;(2)
;(2) .
. ,
, ,则
,则 ( )
( )
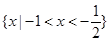


 ,
,
 时,求
时,求 ;
;  ,求实数
,求实数 的取值范围.
的取值范围. ,则
,则 等于 ( )
等于 ( )



 ,则
,则 ( ).
( ).


