题目内容

【题目】在平面直角坐标系中，点，直线：，设圆的半径为1，圆心在上.

（1）若圆心也在直线上，过点作圆的切线，求切线方程；

（2）若圆上存在点，使，求圆心的横坐标的取值范围.

【答案】（Ⅰ）或（Ⅱ）

【解析】试题分析：（1）联立直线与直线，求得圆心坐标，根据点坐标设出切线的方程，由圆心到切线的距离等于圆的半径，列出关于的方程，求出方程的解得的值，确定出切线方程即可；（2）设圆心为，则圆的方程为: ，利用两点间的距离公式列出关系式，得出圆的方程，由在圆上，得到圆与圆相交或相切，根据两圆的半径长，得出两圆的圆心的距离的范围，利用两点间的距离公式列出不等式，求出不等式的解集，即可得到的范围.

试题解析：（1）由得圆心为（3,2）,∵圆的半径为

∴圆的方程为:

显然切线的斜率一定存在,设所求圆C的切线方程为,即

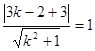∴∴∴∴或者

∴所求圆C的切线方程为:或者即或者

（2）∵圆的圆心在在直线上,所以,设圆心为，

则圆的方程为:

又∵∴设M为（x,y）则整理得:设为圆

∴点M应该既在圆上又在圆上，即圆和圆有交点

∴

由得

由得

终上所述, 的取值范围为

练习册系列答案
相关题目

【题目】某公司生产一批产品需要原材料500吨，每吨原材料可创造利润12万元，该公司通过设备升级，生产这批产品所需原材料减少了吨，且每吨原材料创造的利润提高了；若将少用的吨原材料全部用于生产公司新开发的产品，每吨原材料创造的利润为万元，其中．

（1）若设备升级后生产这批产品的利润不低于原来生产该批产品的利润，求的取值范围；

（2）若生产这批产品的利润始终不高于设备升级后生产这批产品的利润，求的最大值．

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且acosC+ccosA=2bcosA．
（1）求角A的值；
（2）若, ，求△ABC的面积S．

【题目】某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5）， [0.5,1），……[4,4.5]分成9组，制成了如图所示的频率分布直方图.

（I）求直方图中的a值；

（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由；

（Ⅲ）估计居民月均用水量的中位数.

【题目】如图，已知长方形中，为的中点，将 沿折起，使得平面平面．

（1）求证：；

（2）若点是线段上的一动点，问点在何位置时，三棱锥的体积与四棱锥的体积之比为1：3？

【题目】从数列中抽出一项，依原来的顺序组成的新叫数列的一个子列.

（1）写出数列的一个是等比数列的子列；

（2）若是无穷等比数列，首项，公比且，则数列是否存在一个子列，为无穷等差数列？若存在，写出该子列的通项公式；若不存在，证明你的结论.

【题目】在某次测验中，有6位同学的平均成绩为75分， 用xn表示编号为n（n＝1，2，…，6）的同学所得成绩，且前5位同学的成绩如下：

编号n

1

2

3

4

5

成绩xn

70

76

72

70

72

（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s；

（2）从前5位同学中选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．

【题目】某重点高中拟把学校打造成新型示范高中，为此制定了学生“七不准”，“一日三省十问”等新的规章制度．新规章制度实施一段时间后，学校就新规章制度随机抽取部分学生进行问卷调查，调查卷共有10个问题，每个问题10分，调查结束后，按分数分成5组： ，，，，，并作出频率分布直方图与样本分数的茎叶图（图中仅列出了得分在，的数据）．

（1）求样本容量和频率分布直方图中的、的值；

（2）在选取的样本中，从分数在70分以下的学生中随机抽取2名学生进行座谈会，求所抽取的2名学生中恰有一人得分在内的概率．

【题目】调查表明，高三学生的幸福感与成绩，作业量，人际关系的满意度的指标有极强的相关性，现将这三项的满意度指标分别记为，并对它们进行量化：0表示不满意，1表示基本满意，2表示满意．再用综合指标的值评定高三学生的幸福感等级：若，则幸福感为一级；若，则幸福感为二级；若，则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况，研究人员随机采访了该群体的10名高三学生，得到如下结果：

（1）在这10名被采访者中任取两人，求这两人的成绩满意度指标相同的概率；

（2）从幸福感等级是一级的被采访者中任取一人，其综合指标为，从幸福感等级不是一级的被采访者中任取一人，其综合指标为，记随机变量，求的分布列及其数学期望.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网