题目内容
已知向量 =(cosωx-sinωx,sinωx),
=(cosωx-sinωx,sinωx), =(-cosωx-sinωx,2
=(-cosωx-sinωx,2 cosωx),设函数f(x)=
cosωx),设函数f(x)=
 +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1)。
,1)。
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ]上的取值范围。
]上的取值范围。
 =(cosωx-sinωx,sinωx),
=(cosωx-sinωx,sinωx), =(-cosωx-sinωx,2
=(-cosωx-sinωx,2 cosωx),设函数f(x)=
cosωx),设函数f(x)=
 +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1)。
,1)。(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
 ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ]上的取值范围。
]上的取值范围。解:(1)∵f(x)=  ?
? 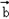 +λ=(cosωx-sinωx)×(-cosωx-sinωx)+sinωx×2
+λ=(cosωx-sinωx)×(-cosωx-sinωx)+sinωx×2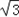 cosωx+λ
cosωx+λ
=-(cos2ωx-sin2ωx)+ 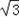 sin2ωx+λ
sin2ωx+λ
= sin2ωx-cos2ωx+λ=2sin(2ωx-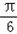 )+λ
)+λ
∵图象关于直线x=π对称,
∴2πω-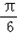 =
=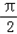 +kπ,k∈z
+kπ,k∈z
∴ω= +
+ ,又ω∈(
,又ω∈( ,1)
,1)
∴k=1时,ω=
∴函数f(x)的最小正周期为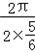 =
=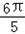 .
.
(2)∵f(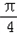 )=0
)=0
∴2sin(2× ×
×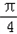 -
-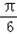 )+λ=0
)+λ=0
∴λ=-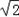
∴f(x)=2sin( x-
x-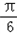 )-
)-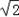
由x∈[0,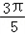 ]
]
∴ x-
x-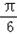 ∈[-
∈[-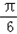 ,
,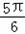 ]
]
∴sin( x-
x-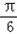 )∈[-
)∈[- ,1]
,1]
∴2sin( x-
x-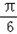 )-
)-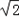 =f(x)∈[-1-
=f(x)∈[-1-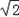 ,2-
,2-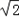 ]
]
故函数f(x)在区间[0,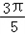 ]上的取值范围为[-1-
]上的取值范围为[-1-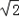 ,2-
,2-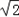 ]。
]。

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |