题目内容
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.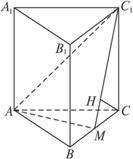
(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离.
(1)证明:∵△AMC1为以点M为直角顶点的等腰直角三角形,
∴AM⊥C1M且AM=C1M.
∵ABC—A1B1C1是正三棱柱,
∴CC1⊥底面ABC.
∴C1M在底面内的射影为CM,AM⊥CM.
∵底面ABC为边长为a的正三角形,
∴点M为BC边的中点.

(2)解:过点C作CH⊥MC1,
由(1)知AM⊥C1M且AM⊥CM,
∴AM⊥平面C1CM.
∵CH⊥AM,
∴CH⊥平面C1AM.
由(1)知AM=C1M=![]() a,CM=
a,CM=![]() a且CC1⊥BC.
a且CC1⊥BC.
∴CC1=![]() =
=![]() a.
a.
∴CH=![]() =
=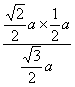 =
=![]() a.
a.
∴点C到平面AMC1的距离为![]() a.
a.

练习册系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.