题目内容
(本小题满分12分)已知函数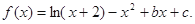 在点x=1处的切线与直线
在点x=1处的切线与直线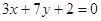 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
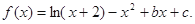 在点x=1处的切线与直线
在点x=1处的切线与直线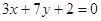 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.f(x)在[0,3]最小值为ln2+5.
本题考查利用导数的性质求函数在闭区间上的最小值,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
与直线3x+7y+2=0垂直的直线的斜率为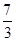
,令f′(1)=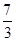 ,得b=4,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,f′(x)=
,得b=4,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,f′(x)= 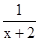 -2x+4,由f′(x)=0,得x=
-2x+4,由f′(x)=0,得x= 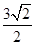 ,由此能求出以f(x)在[0,3]最小值.
,由此能求出以f(x)在[0,3]最小值.
解: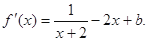 与直线
与直线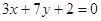 垂直的直线的斜率为
垂直的直线的斜率为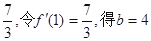 ,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,
,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,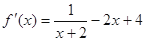 ,由
,由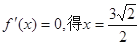 ,当
,当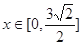 时,f′(x)≥ 0,f(x)单调递增;当
时,f′(x)≥ 0,f(x)单调递增;当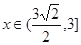 时,f′(x)≤ 0,f(x)单调递减.
时,f′(x)≤ 0,f(x)单调递减.
又f(0)=ln2+5,f(3)=ln5+8,所以f(x)在[0,3]最小值为ln2+5.
与直线3x+7y+2=0垂直的直线的斜率为
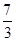
,令f′(1)=
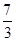 ,得b=4,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,f′(x)=
,得b=4,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,f′(x)= 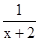 -2x+4,由f′(x)=0,得x=
-2x+4,由f′(x)=0,得x= 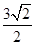 ,由此能求出以f(x)在[0,3]最小值.
,由此能求出以f(x)在[0,3]最小值.解:
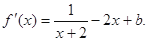 与直线
与直线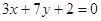 垂直的直线的斜率为
垂直的直线的斜率为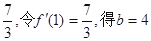 ,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,
,又f(-1)=ln(2-1)-1-4+c=0,所以c=5,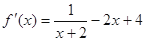 ,由
,由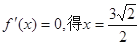 ,当
,当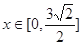 时,f′(x)≥ 0,f(x)单调递增;当
时,f′(x)≥ 0,f(x)单调递增;当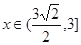 时,f′(x)≤ 0,f(x)单调递减.
时,f′(x)≤ 0,f(x)单调递减.又f(0)=ln2+5,f(3)=ln5+8,所以f(x)在[0,3]最小值为ln2+5.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
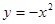 上的点到直线
上的点到直线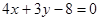 的距离的最小值是
的距离的最小值是 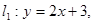
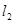 与
与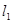 关于直线
关于直线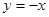 对称,直线
对称,直线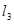 ⊥
⊥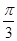 的直线方程;
的直线方程;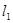 :
: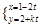 (
( 为参数)与直线
为参数)与直线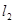 :
: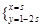 (
(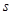 为参数)垂直,则
为参数)垂直,则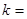 _________________.
_________________.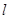 :
: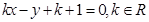 ,则下列结论不正确的是( )
,则下列结论不正确的是( )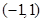
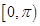
 垂直
垂直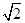
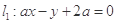 ,
, 互相垂直,则实数
互相垂直,则实数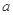 的值是 .
的值是 . 与直线
与直线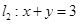 交于P点.
交于P点.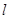 过P点,且与直线
过P点,且与直线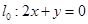 平行时,求直线
平行时,求直线