题目内容
已知二次函数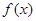 的对称轴方程为:
的对称轴方程为: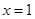 ,设向量
,设向量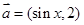 ,
,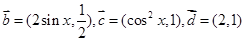 .
.
(1)分别求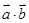 和
和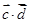 的取值范围;
的取值范围;
(2)当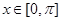 时,求不等式
时,求不等式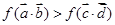 的解集.
的解集.
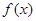 的对称轴方程为:
的对称轴方程为: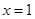 ,设向量
,设向量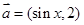 ,
,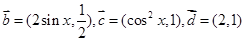 .
.(1)分别求
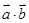 和
和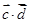 的取值范围;
的取值范围;(2)当
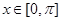 时,求不等式
时,求不等式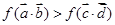 的解集.
的解集.(1) ,
, ;(2)当
;(2)当 时,不等式的解集为
时,不等式的解集为 ;当
;当 时,不等式的解集为
时,不等式的解集为 .
.
 ,
, ;(2)当
;(2)当 时,不等式的解集为
时,不等式的解集为 ;当
;当 时,不等式的解集为
时,不等式的解集为 .
.试题分析:(1)先由平面向量数量积的坐标运算公式计算出
 ,
, ,然后根据正余弦函数的值域,即可得到
,然后根据正余弦函数的值域,即可得到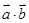 和
和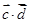 的取值范围;(2)由(1)所求得的范围,与题中条件二次函数
的取值范围;(2)由(1)所求得的范围,与题中条件二次函数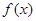 的对称轴方程为:
的对称轴方程为: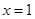 ,分
,分 、
、 两类考虑函数
两类考虑函数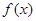 在
在 的单调性,进而将不等式
的单调性,进而将不等式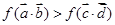 转化为
转化为 、
、 两种情况进行求解,最后结合所给
两种情况进行求解,最后结合所给 的范围与正余弦函数的性质可得原不等式的解集.
的范围与正余弦函数的性质可得原不等式的解集.试题解析:(1)依题意可得
 ,
,
因为
 ,
, ,所以
,所以 ,
, ,所以
,所以 ,
, 即
即 ,
,
(2)
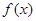 图像关于
图像关于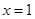 对称
对称当二次项系数
 时,
时,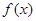 在
在 内单调递增,由
内单调递增,由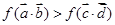 得到
得到 即
即 即
即
又因为

所以
 即
即
当二次项系数
 时,
时,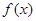 在
在 内单调递减
内单调递减由
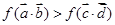 得到
得到 即
即 即
即
又因为

所以
 或
或 即
即 或
或
综上,当
 时不等式的解集为
时不等式的解集为 ;当
;当 时不等式的解集为
时不等式的解集为 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,(1)若
,(1)若 与
与 垂直,求
垂直,求 的值;(2)若
的值;(2)若 ,求
,求 ,则P是△ABC的( )
,则P是△ABC的( )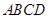 中,
中,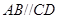 ,
,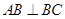 ,
,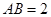 ,
,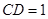 ,
,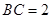 ,
,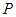 为线段
为线段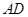 (含端点)上一个动点,设
(含端点)上一个动点,设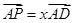 ,
,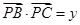 ,对于函数
,对于函数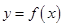 ,给出以下三个结论:①当
,给出以下三个结论:①当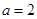 时,函数
时,函数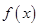 的值域为
的值域为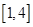 ;
;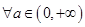 ,都有
,都有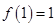 成立;
成立; .
.

 ,其中
,其中 ,
, ,且
,且 ,则向量
,则向量 和
和 的夹角是 .
的夹角是 . ),b=(1,
),b=(1, ,则一定有 ( )
,则一定有 ( ) ,平面内一点
,平面内一点 满足
满足 =
= +
+ ,则
,则 = .
= . 中,
中, ,
, 是边
是边 上一点,
上一点, ,则
,则 =_________.
=_________.