题目内容
已知x∈R+,求函数y=x2(1-x)的最大值.
思路分析:本题积结构中x2=x·x,所以y=x2(1-x)=x×x(1-x),为使“和”为定值,还需拼凑系数.
解:y=x2(1-x)=x·x(1-x)=x·x·(2-2x)×![]()
≤![]() .
.
当且仅当x=2-2x,即x=![]() 时取等号.
时取等号.
此时,ymax=![]() .
.

练习册系列答案
相关题目
已知函数f(x)=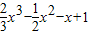 ,x∈R
,x∈R
(1)求函数f(x)的极大值和极小值;
(2)已知x∈R,求函数f(sinx)的最大值和最小值.
(3)若函数g(x)=f(x)+a的图象与x轴有且只有一个交点,求a的取值范围.
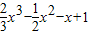 ,x∈R
,x∈R(1)求函数f(x)的极大值和极小值;
(2)已知x∈R,求函数f(sinx)的最大值和最小值.
(3)若函数g(x)=f(x)+a的图象与x轴有且只有一个交点,求a的取值范围.
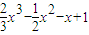 ,x∈R
,x∈R