题目内容
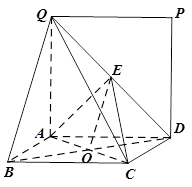
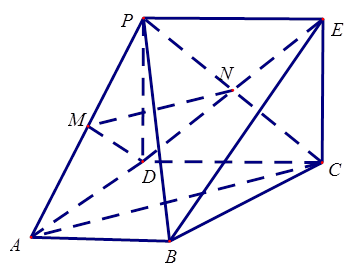
如图,矩形 所在的平面与正方形
所在的平面与正方形 所在的平面相互垂直,
所在的平面相互垂直, 是
是 的中点.
的中点.
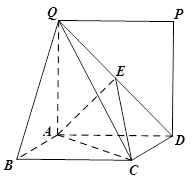
(1)求证: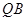 ∥平面
∥平面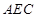 ;
;
(2)求证:平面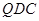 ⊥平面
⊥平面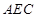 .
.
 所在的平面与正方形
所在的平面与正方形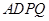 所在的平面相互垂直,
所在的平面相互垂直,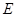 是
是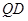 的中点.
的中点.
(1)求证:
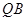 ∥平面
∥平面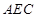 ;
;(2)求证:平面
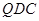 ⊥平面
⊥平面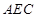 .
.(1)证明详见解析;(2)证明详见解析.
试题分析:(1)要证线面平行,只须在平面内找到一条直线与这条直线平行,对本小题来说,连接
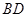 交
交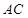 于点
于点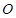 ,由三角形的中位线定理可证得
,由三角形的中位线定理可证得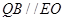 ,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形
,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形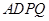 为正方形且
为正方形且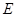 为对角线
为对角线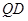 的中点,所以有
的中点,所以有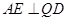 ,故可考虑证明
,故可考虑证明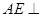 平面
平面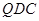 ,故需要在平面
,故需要在平面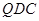 内再找一条直线与
内再找一条直线与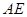 垂直即可,由平面
垂直即可,由平面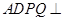 平面
平面 ,交线为
,交线为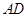 且
且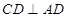 ,从而
,从而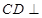 平面
平面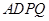 ,可得
,可得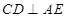 ,从而问题得证.
,从而问题得证.试题解析:(1)连接
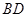 交
交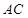 于
于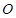 ,连接
,连接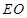
在三角形
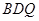 中,
中,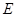 ,
,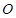 分别为
分别为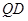 和
和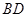 的中点
的中点所以
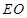 ∥
∥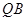 . 2分
. 2分又
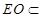 平面
平面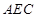 ,
,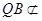 平面
平面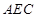
所以
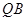 ∥平面
∥平面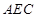 4分
4分(2)因为矩形
 所在的平面与正方形
所在的平面与正方形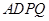 所在的平面相互垂直
所在的平面相互垂直平面
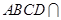 平面
平面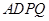 =
=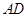 ,
,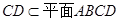 ,
,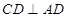
所以
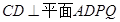
又
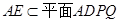 ,所以
,所以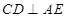 6分
6分又因为
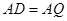 ,
,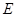 是
是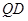 的中点,所以
的中点,所以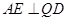
又
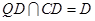 ,所以
,所以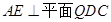 7分
7分由
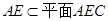 ,所以平面
,所以平面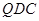 ⊥平面
⊥平面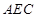 8分.
8分.
练习册系列答案
相关题目
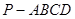 中,底面
中,底面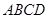 为矩形,
为矩形,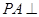 底面
底面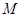 、
、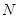 分别是
分别是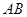 、
、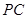 中点.
中点. 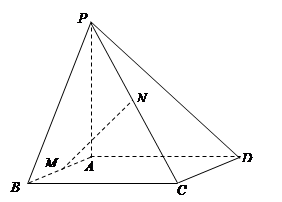
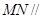 平面
平面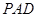 ;
;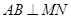 .
.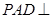 底面
底面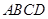 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形,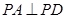 ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.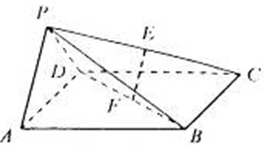
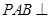 平面
平面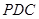 .
.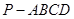 中,底面
中,底面 是边长为
是边长为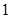 的正方形,
的正方形,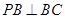 ,
,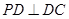 ,且
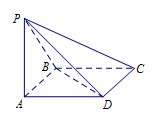
,且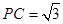 .
.
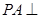 平面
平面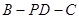 的余弦值;
的余弦值;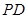 上是否存在一点
上是否存在一点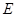 ,使直线
,使直线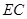 与平面
与平面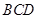 所成的角是
所成的角是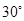 ?若存在,求
?若存在,求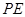 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.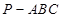 中,
中,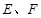 分别为
分别为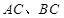 的中点.
的中点.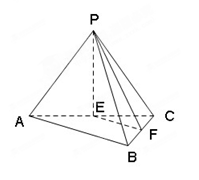
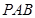 ;
;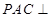 平面
平面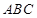 ,且
,且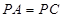 ,
,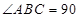 º,求证:平面
º,求证:平面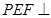 平面
平面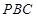
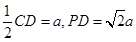 .
.
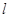 表示一条直线,
表示一条直线,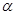 ,
,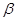 表示两个不重合的平面,有以下三个语句:①
表示两个不重合的平面,有以下三个语句:①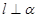 ;②
;②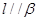 ;③
;③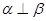 .以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
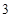
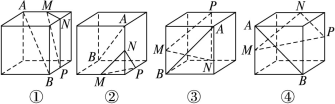
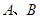 为正方体的两个顶点,
为正方体的两个顶点,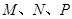 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出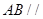 平面
平面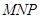 的图形的序号是( )
的图形的序号是( )