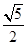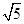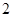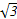题目内容
已知双曲线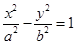 (
( ,
,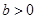 ),过其右焦点且垂直于实轴的直线与双曲线交于
),过其右焦点且垂直于实轴的直线与双曲线交于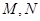 两点,
两点,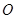 为坐标原点,若
为坐标原点,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.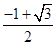 | B.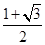 | C.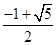 | D.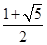 |
D
解析试题分析:画出图形,根据双曲线的对称性及 ,可得
,可得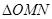 是等腰直角三角形(不妨设点
是等腰直角三角形(不妨设点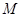 在第一象限),
在第一象限),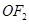 平分角
平分角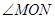 ,所以
,所以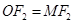 ,即
,即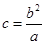 (因为由
(因为由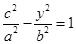 得到
得到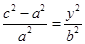 ,所以
,所以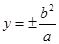 ),所以
),所以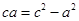 ,整理得
,整理得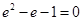 ,解得
,解得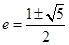 .由双曲线
.由双曲线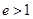 ,可得
,可得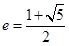 ,故选D.
,故选D.
考点:离心率 双曲线

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
设椭圆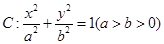 的左、右焦点分别为
的左、右焦点分别为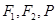 是
是 上的点
上的点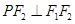 ,
,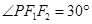 ,则椭圆
,则椭圆 的离心率为( )
的离心率为( )
A.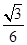 | B.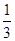 | C.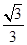 | D. |
顶点在原点,准线与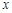 轴垂直,且经过点
轴垂直,且经过点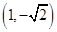 的抛物线方程是( )
的抛物线方程是( )
A.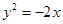 | B.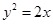 | C.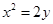 | D.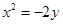 |
在 中,
中,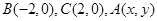 ,给出
,给出 满足的条件,就能得到动点
满足的条件,就能得到动点 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
| 条件 | 方程 |
① 周长为10 周长为10 | 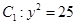 |
② 面积为10 面积为10 | 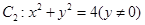 |
③ 中, 中,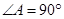 | 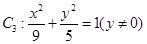 |
 轨迹方程按顺序分别是
轨迹方程按顺序分别是 A.
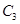 、
、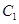 、
、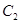 B.
B. 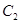 、
、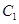 、
、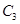
C.
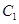 、
、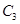 、
、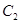 D.
D. 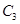 、
、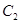 、
、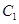
与椭圆C: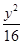 +
+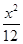 =1共焦点且过点(1,
=1共焦点且过点(1,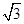 )的双曲线的标准方程为( )
)的双曲线的标准方程为( )
A.x2-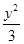 =1 =1 | B.y2-2x2=1 |
C.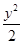 - -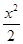 =1 =1 | D.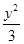 -x2=1 -x2=1 |
已知F1,F2分别是双曲线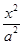 -
-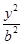 =1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若
=1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若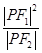 =8a,则双曲线的离心率的取值范围是( )
=8a,则双曲线的离心率的取值范围是( )
| A.(1,2] | B.[2,+∞) |
| C.(1,3] | D.[3,+∞) |
抛物线y2=4x的焦点到双曲线x2-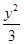 =1的渐近线的距离是( ).
=1的渐近线的距离是( ).
A. | B.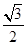 | C.1 | D.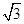 |
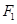 、
、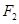 是双曲线
是双曲线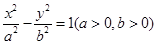 的左、右焦点,若双曲线左支上存在一点一点
的左、右焦点,若双曲线左支上存在一点一点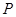 与点
与点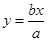 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )