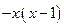题目内容
(本题满分12分)函数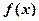 是R上的偶函数,且当
是R上的偶函数,且当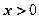 时,函数的解析式为
时,函数的解析式为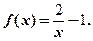
(1)求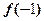 的值;
的值;
(2)用定义证明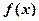 在
在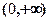 上是减函数;
上是减函数;
(3)求当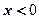 时,函数的解析式;
时,函数的解析式;
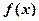 是R上的偶函数,且当
是R上的偶函数,且当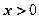 时,函数的解析式为
时,函数的解析式为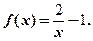
(1)求
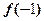 的值;
的值; (2)用定义证明
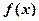 在
在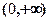 上是减函数;
上是减函数;(3)求当
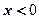 时,函数的解析式;
时,函数的解析式;(1)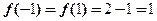
(2)略
(3)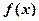 =
=
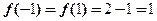
(2)略
(3)
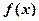 =
=
解: (1)因为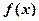 是偶函数,所以
是偶函数,所以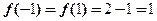 ;--------4分
;--------4分
(2) 设x1,x2是(0,+∞)上的两个任意实数,且x1 <x2,
又 f (x1)- f (x2) = -2- (
-2- ( -2) =
-2) = -
- =
= .
.
因为x2- x1 >0,x1x2 >0 , 所以f (x1)> f (x2)
因此f (x) =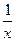 -2是(0,+∞)上的减函数. ------------8分.
-2是(0,+∞)上的减函数. ------------8分.
(3)设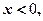 则
则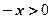 ,所以
,所以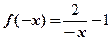 ,又
,又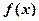 为偶函数,所以
为偶函数,所以
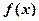 =
= .--------------12分
.--------------12分
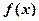 是偶函数,所以
是偶函数,所以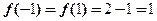 ;--------4分
;--------4分(2) 设x1,x2是(0,+∞)上的两个任意实数,且x1 <x2,
又 f (x1)- f (x2) =
 -2- (
-2- ( -2) =
-2) = -
- =
= .
.因为x2- x1 >0,x1x2 >0 , 所以f (x1)> f (x2)
因此f (x) =
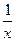 -2是(0,+∞)上的减函数. ------------8分.
-2是(0,+∞)上的减函数. ------------8分.(3)设
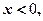 则
则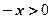 ,所以
,所以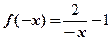 ,又
,又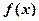 为偶函数,所以
为偶函数,所以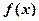 =
= .--------------12分
.--------------12分
练习册系列答案
相关题目
 时,y=x;当x>2时,y=f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分
时,y=x;当x>2时,y=f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分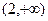 上的解析式;
上的解析式;
 当
当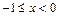 时,
时,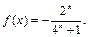
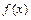 在[-1,1]上的解析式;
在[-1,1]上的解析式;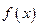 的定义域为
的定义域为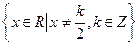 ,且
,且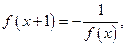 如果
如果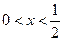 时,
时,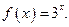
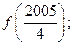
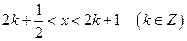 时,求
时,求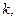 使得当
使得当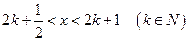 时,
时,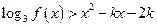 有实数解.
有实数解.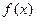 既是奇函数,又是周期为3的周期函数,当
既是奇函数,又是周期为3的周期函数,当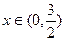 时,
时,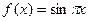 ,
,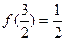 ,则函数
,则函数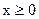 时,
时,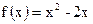 , 则
, 则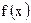 在
在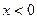 时的解析式是 _______________
时的解析式是 _______________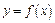 是偶函数,而
是偶函数,而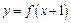 是奇函数,且对任意
是奇函数,且对任意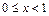 ,都有
,都有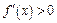 ,则
,则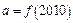 ,
,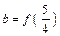 ,
,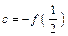 的大小关系是
的大小关系是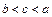
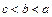
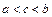

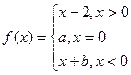 是奇函数,则
是奇函数,则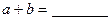 .
.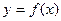 为奇函数,当
为奇函数,当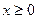 时
时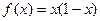 ,则当
,则当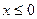 时,
时, 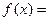 (
( )
)
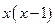 B
B 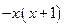 C
C  D
D