Question

【题目】试求正数的最大值，使得点集一定被包含于另一个点集，且对任何，都有之中．

Answer 1

【答案】

【解析】

集即为由直线确定的上半平面的交集（不同，相对应的上半平面一般也不同，但所有的这种上半平面有公共部分即交集；另外，可以规定上半平面也包含了这条直线）．而半径为的圆的圆心到直线的距离为．

由题意知，应满足．故的最大值是的最小值．

而

，

等号成立当且仅当，即时成立．

故．

另解：把等价地改写为．

令，则．

下而分两种情形讨论的情况：

（1）若对称轴或即或）时，

只须当时有，

即（或）． ①

（2）若对称轴，即时，只须判别式，

即． ②

以上的①和②刻画了集①和②}．

设圆与抛物线相切，消去得，即．

令其判别式得，解得．

此时，．

而点到直线的距离为（如图），

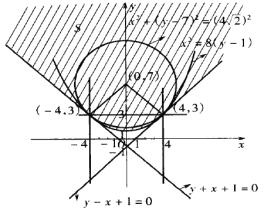
故由上述结果可知．（不能再大，否则越出的区域）．

注：区域是图中的阴影部分．