题目内容
已知斜率为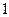 的直线
的直线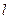 过抛物线
过抛物线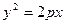
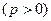 的焦点
的焦点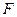 ,且与抛物线交于
,且与抛物线交于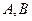 两点,(1)求直线
两点,(1)求直线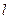 的方程(用
的方程(用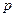 表示);
表示);
(2)若设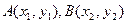 ,求证:
,求证: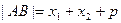 ;
;
(3)若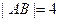 ,求抛物线方程.
,求抛物线方程.
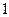 的直线
的直线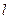 过抛物线
过抛物线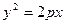
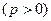 的焦点
的焦点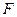 ,且与抛物线交于
,且与抛物线交于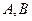 两点,(1)求直线
两点,(1)求直线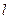 的方程(用
的方程(用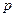 表示);
表示);(2)若设
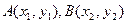 ,求证:
,求证: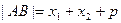 ;
;(3)若
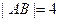 ,求抛物线方程.
,求抛物线方程. |
(1)直线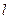 的方程为:
的方程为: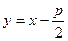 .(2)同解析,(3)抛物线方程
.(2)同解析,(3)抛物线方程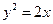 .
.
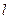 的方程为:
的方程为: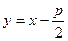 .(2)同解析,(3)抛物线方程
.(2)同解析,(3)抛物线方程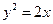 .
.(1)∵抛物线的焦点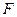 的坐标为
的坐标为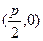 ,
,
又∵直线的斜率为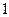
∴直线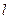 的方程为:
的方程为: .
.
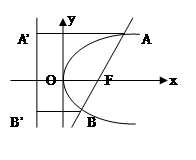 (2)证明:过点A,B分别作准线的垂线
(2)证明:过点A,B分别作准线的垂线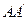 ,
,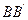 ,
,
交准线于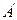 ,
,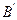 ,则由抛物线的定义得:
,则由抛物线的定义得:
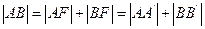
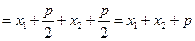 .
.
(3)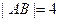 ,
, ,直线
,直线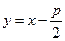 与抛物线方程联立,
与抛物线方程联立,
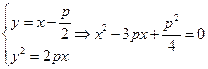 ,由韦达定理,
,由韦达定理, ,
,
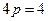 ,
,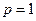 ,抛物线方程
,抛物线方程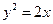 .
.
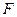 的坐标为
的坐标为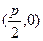 ,
,又∵直线的斜率为
∴直线
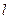 的方程为:
的方程为: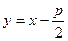 .
.  (2)证明:过点A,B分别作准线的垂线
(2)证明:过点A,B分别作准线的垂线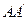 ,
,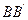 ,
,交准线于
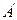 ,
,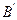 ,则由抛物线的定义得:
,则由抛物线的定义得: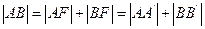
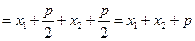 .
.(3)
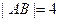 ,
, ,直线
,直线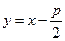 与抛物线方程联立,
与抛物线方程联立,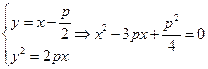 ,由韦达定理,
,由韦达定理, ,
,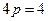 ,
,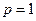 ,抛物线方程
,抛物线方程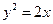 .
.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

 的离心率为
的离心率为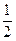 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线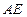 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.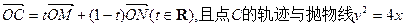 交于A、B两点。
交于A、B两点。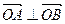 ;
;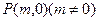 ,使得过点P的直线l交抛物线
,使得过点P的直线l交抛物线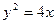 于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。
于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。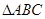 的两个顶点坐标A
的两个顶点坐标A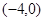 、B
、B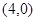 ,
,



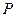 与平面上两定点
与平面上两定点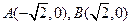 连线的斜率的积为定值
连线的斜率的积为定值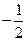 .
.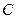 ;
;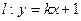 与曲线
与曲线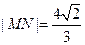 时,求直线
时,求直线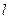 的方程.
的方程.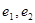 分别为具有公共焦点
分别为具有公共焦点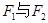 的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足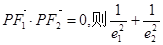 的值为 ( )
的值为 ( )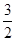
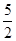
 与椭圆
与椭圆 交于A、B两点,记△ABO的面积为S.
交于A、B两点,记△ABO的面积为S.
 ,则当
,则当 取最小值时,椭圆
取最小值时,椭圆 的离心率是( )
的离心率是( )



 的左、右焦点分别为
的左、右焦点分别为 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在该双曲线上,则
在该双曲线上,则