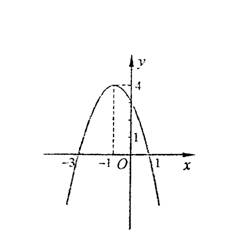
题目内容
(本小题14分)
函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+f(b)-1,
并且当x＞0时，f(x)＞1.
（1）求证：f(x)是R上的增函数；
（2）若f(4)=5,解不等式f(3m2-m-2)＜3.
(本小题14分)
解 （1）设x1,x2∈R，且x1＜x2,
则x2-x1＞0,
∴f(x2-x1)＞1………………………………………………………2分
f(x2)-f(x1)=f((x2-x1)+x1)-f(x1)
=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1＞0……………………………5分.
∴f（x2）＞f(x1).
即f(x)是R上的增函数. …………………………………………7分.
（2）∵f（4）=f（2+2）=f（2）+f（2）-1=5，
∴f（2）=3，……………………………………………………10分 ∴原不等式可化为f(3m2-m-2)＜f(2),
∵f(x)是R上的增函数，∴3m2-m-2＜2, ………………………12分
解得-1＜m＜
,故解集为（-1, ）. ………………………14分
，如果满足；对任意
，存在常数
，都有
成立，则称
，
当
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；若
，求函数
在
上的上界T的取值范围。
.
的最小正周期；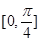
上的函数值的取值范围.
的单调性；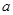
的取值范围；
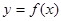对于区间D上的任意两个值x1、x2总有以下不等式
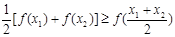成立，则称函数
，试判断函数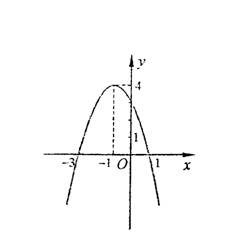
（2）求使函数值取非负值的x的集合；