题目内容
已知集合 ,
, ,则
,则 = .
= .

【解析】
试题分析:因为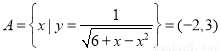 ,
, ,则
,则
 ,所以
,所以 .故填
.故填 .
.
考点:函数定义域和集合的补集、交集运算.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
题目内容
已知集合 ,
, ,则
,则 = .
= .

【解析】
试题分析:因为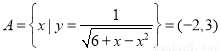 ,
, ,则
,则
 ,所以
,所以 .故填
.故填 .
.
考点:函数定义域和集合的补集、交集运算.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案