题目内容
已知F1、F2是双曲线4x2(1)求曲线C的方程;
(2)过F2作一直线l交曲线C于A、B两点,若 2![]() =
=![]() +
+![]() ,求△MF2O面积最大时直线l的方程.
,求△MF2O面积最大时直线l的方程.
解:(1)双曲线4x2![]() y2=1的左、右焦点分别是F1(-1,0)、F2(1,0).
y2=1的左、右焦点分别是F1(-1,0)、F2(1,0).
由|![]() |+|
|+|![]() |=4>2得曲线C是以F1、F2为焦点、长轴长为4的椭圆.
|=4>2得曲线C是以F1、F2为焦点、长轴长为4的椭圆.
∴2c=2,2a=4.∴c=1,a=2,b=![]() .
.
∴曲线C的方程为![]() =1.
=1.
(2)由2![]() =
=![]() +
+![]() 可知点M是线段AB的中点,设其坐标为(x0,y0).
可知点M是线段AB的中点,设其坐标为(x0,y0).
①若直线l的斜率不存在,则直线l的方程是x=1,此时,点M与F2重合,不能构成三角形.②若直线的斜率存在,设为k,且k≠0,则直线l的方程是y=k(x-1).
联立方程组得
将(i)代入(ii),整理得(3+4k2)x2-8k2x+4(k2-3)=0.
设A(x1,y1),B(x2,y2),由韦达定理可得x1+x2=![]() ,
,
∴x0=![]() (x1+x2)=
(x1+x2)=![]() .
.
又∵M在直线l上,∴y0=k(x0-1)=k(![]() -1)=
-1)=![]() .
.
∴![]() =
=![]() ×|OF2|×|y0|=
×|OF2|×|y0|=![]() ×1×
×1×![]() =
=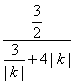 .
.
∵![]() +4|k|≥2
+4|k|≥2![]() |k|=43(当且仅当
|k|=43(当且仅当![]() =4|k|,即k=±
=4|k|,即k=±![]() 时,等号成立).
时,等号成立).
∴![]() 2≤
2≤![]() =
=![]() .
.
此时直线方程为y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1),即
(x-1),即![]() x-2y-
x-2y-![]() =0或
=0或![]() x+2y-
x+2y-![]() =0.
=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
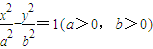 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若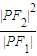 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )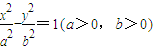 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若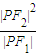 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )