题目内容
已知函数![]() ,
,![]()
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若在![]() (
(![]() )上存在一点
)上存在一点![]() ,使得
,使得![]()
![]()
![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
解:(1)![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
|
|
| 1 |
|
|
| — | 0 | + |
|
|
| 极小 |
|
所以![]() 在
在![]() 处取得极小值1.
处取得极小值1.
(2)![]() ,
,
![]()
①当![]() 时,即
时,即![]() 时,在
时,在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,
,
所以,函数![]() 在
在![]() 上单调递增.
上单调递增.
(3)在![]() 上存在一点
上存在一点![]() ,使得
,使得![]()
![]()
![]() 成立,即在
成立,即在![]() 上存在一点
上存在一点![]() ,
,
使得![]() ,即函数
,即函数![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
由(2)可知
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 的最小值为
的最小值为![]() ,由
,由![]() 可得
可得![]() ,
,
因为![]() ,所以
,所以![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 最小值为
最小值为![]() ,由
,由![]() 可得
可得![]() ;
;
③当![]() ,即
,即![]() 时, 可得
时, 可得![]() 最小值为
最小值为![]() ,
,
因为![]() ,所以,
,所以,![]()
故![]()
此时,![]() 不成立.
不成立.
综上讨论可得所求![]() 的范围是:
的范围是:![]() 或
或![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为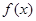 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素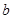 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程