题目内容

已知函数f（x）=x（2-|x|），则函数y=f（x）的增区间是
 
．
分析：根据函数的单调性的判定方法直接进行判断即可，首先将函数的解析式化简，写成分段函数的形式，然后借助于函数的图象进行求解．
解答：解：∵f（x）=x（2-|x|）=
-x2+2x，x≥0
x2+2x，x＜0
，
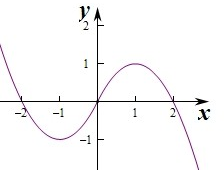
∴对应的图象如图：精英家教网
则函数的增区间为[-1，1]，
故答案为：[-1，1]．
点评：本题主要考查函数单调性的判断，理解分段函数的单调性的处理方法，对绝对值的处理思路和方法．
练习册系列答案
相关题目
精英家教网已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式是（　　）
A、f(x)=2sin(πx+
π
6
)(x∈R)
B、f(x)=2sin(2πx+
π
6
)(x∈R)
C、f(x)=2sin(πx+
π
3
)(x∈R)
D、f(x)=2sin(2πx+
π
3
)(x∈R)
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网